Поэтому получаем уравнение

которое имеет решение

2 . L Со - Gz.

3 pGo

(8.9)

(8.10)

Поскольку Go>Gl, получаем, что правая часть этого уравнения положительна, когда р<0, что согласуется с качественным доказательством, приведенным выше.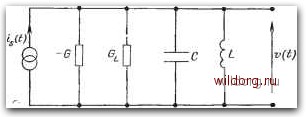

Рис. 8.2. Эквивалентная схема генератора колебаний, иа который действует внешний источник тока.

Заметим, что коэффициент а линейного члена в выражении (8.2) отсутствует в выражении для амплитуды стационарных колебаний: их уровень определяется величиной коэффициента р квадратичного члена. При уменьшении квадратичной нелинейности в характеристике проводимости амплитуда свободных колебаний генератора возрастает в соответствии с обратной зависимостью в формуле (8.10).

Угловая частота собственных колебаний Ио равна угловой резонансной частоте колебательного контура генератора на рис. 8.1, т. е. Ио=1/У/-С. Этот результат вытекает из решения уравнения (8.4), проведенного ван-дер-Полем.

8.3. Вынужденные колебания

На рис. 8.2 показана эквивалентная схема генератора колебаний, на который действует внешний генератор тока. Внешний источник может оказывать сильное влияние на выходной сигнал генератора. Дифференциальное уравнение для выходного напряжения в данном случае является неоднородным вари-

антом уравнения (8.4), правая часть которого содержит член с источником:

(8.11)

Как и прежде, именно от квадратичного члена в нелинейной проводимости (т. е. кубического члена по току) зависят особенности поведения генератора колебаний.

Решение уравнения (8.11) подробно проведено ван-дер-Полем [17] для случая воздействия на генератор гармонического сигнала. Как и следовало ожидать, этот анализ трудоемкий, но здесь мы только кратко подытожим наиболее важные выводы. Существуют два фактора, значительно влияющие на вид выходного напряжения: амплитуда внешнего воздействия и частота внешнего воздействия, отнесенная к резонансной частоте контура.

Когда частота внешнего источника близка к частоте свободных колебаний, выходной сигнал генератора синхронизован по фазе и частоте с источником и собственные колебания полностью подавлены при условии, что амплитуда источника достаточно высока. Вне полосы частот, в пределах которой наблюдается частотная синхронизация, внешний источник слабо влияет на выходной сигнал, который в этом случае почти целиком состоит из собственных колебаний.

Следует подчеркнуть, что спектральная ширина области частотной синхронизации зависит от уровня амплитуды внешнего генератора. Если бы вместо гармонического сигнала имелось шумовое воздействие, явления синхронизации частоты не было бы, так как в любой реальной схеме энергия источника шума за время когерентности флуктуации по величине на много порядков меньше, чем энергия свободных колебаний. Таким образом, при наличии шумового генератора свободные колебания сохраняются, но их амплитуда и фаза подвержены случайным флуктуациям. Эти флуктуации - предмет дальнейшего обсуждения в данной главе.

8.4. Выходной шум

Как было сказано выше, источник собственного шума генератора ван-дер-Поля обычно можно представить единственным генератором шуыа, как показано на рис. 8.3. Это не самое общее представление, но оно подходит для большинства твердотельных генераторов с отрицательной проводимостью. В устройстве на эффекте Ганна, например, шумовой генератор in{t) на рис. 8.3 обычно представляет неравновесный шум Джонсона

популяции горячих электронов вне движущегося домена (см. гл. 10).

Некоторые авторы исследовали влияние шума на выходной сигнал генератора, причем большинство из них предполагали, что in{t) -источник белого шума [3, 5, 7-9]. Анализ, проведенный в работах [7, 8], был расширен в работе [Ю], чтобы включить в рассмотрение 1 -шум. Рассмотрим кратко этапы анализа, вновь предполагая, что in{t) имеет равномерный спектр мощности, так как это допущение несколько упрощает

v(t)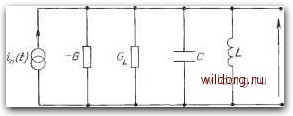

Рис. 8.3. Эквивалентная схема генератора колебаний, собственный шум которого представлен параллельным шумовым генератором тока.

выкладки. Кроме того, это действительно имеет место в ряде реальных твердотельных генераторов.

Выходное напряжение генератора шума, изображенного на рис. 8.3, является решением неоднородного уравнения

(8.12)

где правая часть описывает источник белого шума, а G - нелинейная проводимость, определяемая выражением (8.2). Из-за наличия нелинейных членов решение этого уравнения в общем виде получить трудно. Как и во многих нелинейных задачах, обычный путь - найти приближенное решение, применяя метод линеаризации, но даже в этом случае анализ достаточно сложен.

Шум двояко влияет на собственные колебания на выходе: он модулирует амплитуду и вносит случайно флуктуирующий фазовый сдвиг. Таким образом, выходное напряжение можно представить в виде

. f (0 = Uo[i+«(01cosK--ф(0], (8.13)

где член а (t) описывает модуляцию амплитуды, т]5 (t) - модуляцию фазы, а ио - амплитуда собственных колебаний в отсутствие шума, значение которой задается уравнением (8.10). Функции a{t) и {t) соответствуют стационарным стохастическим процессам, а так как генератор имеет чрезвычайно узкую