6.7. Физические механизмы возникновения 1 -шума и его теоретические модели

Выше мы рассмотрели свойства l/f-шума как статистического процесса, характер некоторых форм сигналов, приводящих к l/f-спектрам, и некоторые экспериментальные данные по исследованию l/f-флуктуаций. На этом фоне теперь уместно проанализировать некоторые из предложенных теоретических моделей этого явления. Легко видеть, что расхождения, а в некоторых случаях очевидное несоответствие результатов экспериментальных исследований очень сильно затрудняют построение удовлетворительной теоретической модели. И в самом деле, такой модели сейчас не существует. Моделям, которые имеются, в значительной мере недостает универсальности описания. Мы начнем с рассмотрения очень частного и скорее необычного случая l/f-шума.

6.7.1. l/f-шум в конденсаторе с потерями

Эквивалентную схему конденсатора с потерями можно представить емкостью С, включенной параллельно резистору R, который характеризует эти диэлектрические потери (рис. 6.4). Резистор обладает тепловым шумом, в этой схеме представлен-

энергетические уровни играют важную роль в процессе проводимости.

Во всех случаях исследованные 1/f-спектры шума у аморфных и поликристаллических материалов точно пропорциональны квадрату величины постоянного тока и имеют зависимость от частоты, близкую к f-. У некоторых типов стекол уровень l/f-шума не зависит от температуры. Это обнаружили Сойер и Прасад [55] для ванадиево-фосфатного стекла в интервале температур 77-300 К. Кроме того, они нашли, что в данном температурном диапазоне величина проводимости увеличивается на 6 порядков, тогда как число носителей, определенное из измерений электронного спинового резонанса, остается постоянным. Скрытый смысл состоит в том, что такое изменение проводимости обусловлено изменением подвижности, и поскольку оно не сопровождается изменением шума, то, по-видимому, это является дополнительным доводом против гипотезы о том, что l/f-шум обусловлен флуктуациями подвижности носителей, которые, по всей вероятности, должны расти с увеличением подвижности.

ным подключенным параллельно токовым генератором шума; in{t), который обусловливает флуктуации напряжения и„() на выходных клеммах в случае разомкнутой цепи. Ван-дер-Зил [62] отмечал, что в том случае, когда тангенс угла потерь не зависит от частоты, шум выходного напряжения имеет спектр 1 . Это аргументируется следующим образом.

Если комплексная диэлектрическая постоянная диэлектрического материала с потерями, находящегося в конденсаторе.

v„(t)

Рис. 6.4. Эквивалентная схема конденсатора с диэлектрическими потерями.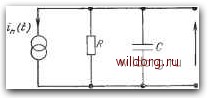

составляет б = б--/е , то тангенс угла диэлектрических потерь определяется выражением

tg6 = e7e, (6.31)

а полная проводимость параллельной 7?С-цепочки - выражением

Г = усй(е-/е")еоЛ/, (6.32).

где А Vi d - площадь поперечного сечения и толщина диэлектрического слоя соответственно. Из сравнения уравнения (6.32) с выражением для полной проводимости эквивалентной цепи, изображенной на рис. 6.4, можно получить следующие выражения для величин емкости и сопротивления:

C = ггoAd, R=

(6.33)

(6.34)

е"8ошЛ

а если использовать уравнение (6.31), то

= (oCtg6

Далее, спектральная плотность токового генератора теплового шума описывается уравнением

57й = 4Щ/?, (6.35)

а флуктуации напряжения - уравнением

(6.36)

S„ И = j~- sin б cos б, (6.37)

т. е. когда угол потерь б не зависит от частоты, имеет место ;зaкoн l/f.

Это условие не выполняется на низких частотах, когда со-:Противление потерь просто определяется проводимостью о диэлектрика

R = d/GA. (6.38)

Так как данное выражение не зависит от частоты, тангенс угла потерь в выражении (6.34) обратно пропорционален часто-;те и, следовательно, функция 5о((й) в выражении (6.37) имеет зависимость от ш в виде (l-f-o/C)-. Поэтому шум конденсатора, обладающего диэлектрическими потерями, на очень низких частотах не описывается -спектром.

Однако, согласно наблюдениям, на высоких частотах, когда потери определяются эффектами диэлектрической релаксации, tg6 по существу не зависит от частоты. Этот факт трудно объяснить, используя единичное время релаксации; он может быть обусловлен некоторым распределением времен релаксации. Од-•На из возможных функций распределения, которая приводит к отсутствию зависимости от частоты угла потерь в ограниченном диапазоне частот, была рассмотрена ван-дер-Зилом [64]. Таким образом, можно сказать, что в ограниченном диапазоне частот уравнение ,(6.37) описывает зависимость l/\f\. Здесь :мы не повторяем доводы ван-дер-Зила, поскольку они в основ-ном такие же, за исключением мелких деталей, приводимых ниже в связи с рассмотрением 1 -шума в полупроводниках с некоторым распределением времен жизни носителей на ловуш-.ках.

6.7.2. Захват носителей поверхностными ловушками в полупроводниках

Очевидно, самой распространенной моделью 1 -шума следует считать модель, основанную на захвате носителей ловуш-ками с :Ш«роким интервалом времен жизни носителей. Идея, ;которая применима для случая полупроводниковых материалов, следующая. Когда свободный носитель теряет свою свободу, попадая на центр рекомбинации или в ловушку, то он в течение некоторого времени не принимает участия в проводимости и это приводит к соответствующей модуляции сопротивления .образца. Если считать, что процесс подобного захвата подчини-

Комбинируя эти три последних уравнения, получаем