
 |
|
Главная страница Математические методы [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [ 51 ] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] форм таких импульсов. Но в общем очевидно, что к этому процессу проявлен слабый интерес, исключение составляет работа Белла [9], который рассмотрел модель подобного типа. Другое математическое представление сигнала 1 , рассматриваемое ниже, основано на суперпозиции большого числа релаксационных процессов с широкой вариацией характерных постоянных времени {50, 61]. Эта модель получила широкое признание, что, по всей вероятности, связано с ее непосредственным отношением к поверхностному механизму 1 -шума в МОП ПТ, согласно которому носители туннелируют между полупроводником и ловушками, локализованными в слое окисла. -Обобщение модели суперпозиции описано в работе [24]. f6.4.1. Модель l/f-шума, основанная на процессе случайного цуга импульсов Используя теорему Карсона (разд. 2.6), можно получить выражение для спектральной плотности случайного цуга импульсов x{t) при форме единичного импульса, заданного функцией f{t): S)==2vaF{iisi)f, (6.14) тде F(/ki) - преобразование Фурье функции /(/); - средний .квадрат высоты импульса, а v - средняя частота следования импульсов. Анализ уравнения (6.14) показывает, что частотная зависимость Sx полностью определяется формой отдельного импульса f{t). Следовательно, вопрос состоит в выборе такой формы отдельного импульса в цуге, которая приведет к нужной спектральной функции, а именно l/f". (Подобный вопрос уже встречался при рассмотрении теплового и дробово--го шума, где в тех же случаях для формы импульса использовали дельта-функцию, ее преобразование равно единице и спектры не зависят от частоты.) Будем считать, что форма отдельного импульса в цуге описывается функцией f{t) = u if) t- (-«/2 ехр -luj, (6.15) где а я (i)x - оба положительны и не зависят от времени; а - приближенно, но не точно равно единице, а u{t)-единичная ступенчатая функция. Фурье-преобразование функции /(f) опи-.сывается формулой /Г(у(0)= j-(l-a/2)exp-(«,+/«)= 1ML ., (6.16) где Г( )-гамма-функция. Интеграл в выражении (6.16) имеет стандартную форму и его значение можно найти в любой таблице, например в работе [23]. Если результат, полученный из уравнения (6.16), подставить в выражение теоремы Карсона, то найдем, что спектральная плотность процесса, моделируемого случайным цугом импульсов с формой отдельного импульса, заданного выражением (6.15), имеет вид S.(«) = 2var (и/2) (6.17) Кривая, характеризующая зависимость (6.17) представлена на рис. 6.1,0. Из этого рисунка видно, что имеется граничная ча- 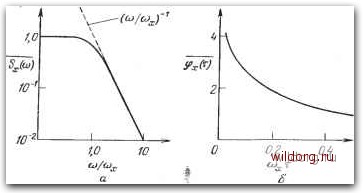 Рис. 6.1. о - спектральная плотность рассчитанная нз уравнения (6.17) и нормализованная к нулевому значению частоты при а=1; б - соответствующая автокорреляционная функция, рассчитанная из уравнения (6.19) прн с=2п. стота со = со;с, ниже которой кривая по существу параллельна оси абсцисс, а в диапазоне, где соЮл;, можно провести аппроксимацию 5лг(со) следующим образом: 5.(«)- а=1, (6.18) где c=2vor(a/2). Такая спектральная зависимость соответствует реально наблюдаемым спектрам l/f-шума даже вплоть до возможности некоторого изменения логарифмического наклона за счет показателя а. Более того, закон обратной степенной зависимости можно использовать в любом сколь угодно широком диапазоне частот, так как величину граничной (угловой) частоты (Их, входящей в выражение (6.17), можно выбрать сколь угодно малой. К тому же ясно, что сколь бы малым ни было значение Юлг (при условии, однако, что оно не обращается в нуль), функция Sx(iu) в уравнении (6.17) удовлетворяет условию стационарности (в широком смысле), неявно содержащемуся в уравнении (6.10). Если считать, что а>х находится значительно ниже наблюдаемого диапазона частот, то автокорреляционная функция и значение среднего квадрата x{t) будут зависеть от времени измерения Т, как это обсуждалось в разд. 6.3.3.. С теоретической точки зрения представляет интерес проанализировать изменение этих статистических характеристик в пределе при Т->-оо. в этом случае для получения автокорреляционной функции в интеграл Винера - Хинчина целесообразно подставить спектральную плотность в виде, описываемом уравнением (6.17), а не уравнением (6.18): = 1" ) = 0 («..T). (6.19) где с целью упрощения используется коэффициент а, равный единице, а Ко (мт) - модифицированная функция Бесселя второго рода нулевого порядка. График зависимости функции фл:(т) от юлгт приводится на рис. 6.1,6. Возможно смысл автокорреляционной функции легче понять, если аппроксимировать данную функцию Бесселя суммой первых трех членов ее разложения в ряд о(2) = -Т+1п(2)-1п(г)+..., (6.20) где у=0,5772... - постоянная Эйлера. Для случая малых которые нас и интересуют, очевидно, функция флг(т) изменяется как 1п(солгт), причем для фхО она конечна во всех точках по т, за исключением начала координат, где она имеет логарифмическую неопределенность, связанную с высокочастотной границей спектра l/f-шума. Но это не большая помеха, чем дельта-функция, входящая в автокорреляционную функцию для белого шума, спектр которого распространен равномерно до бесконечности: в обоих случаях бесконечность среднего квадрата есть не что иное, как математическая абстракция, так как в реальной ситуации ограничения полосы пропускания приводят к конечным значениям этих величин. В случае же когда юлг=0, легко видеть из уравнений (6.19) и (6.20), что автокорреляционная функция является неопределенной при любом значении т. Несомненно, что такое странное с теоретической точки зрения свойство связано с применимостью формулы 1/1 fl вплоть до крайне малых значений частоты; и хотя для 1 -шума следует ожидать крайне больших значений времени [0] [1] [2] [3] [4] [5] [6] [7] [8] [9] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [ 51 ] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] [79] [80] [81] [82] [83] [84] [85] [86] [87] [88] [89] [90] [91] [92] [93] [94] [95] [96] [97] [98] [99] [100] [101] [102] [103] [104] [105] [106] [107] [108] [109] [110] [111] [112] [113] [114] [115] [116] [117] [118] [119] [120] [121] [122] [123] [124] [125] [126] [127] [128] [129] 0.015 |