ПТс р-п-переходом

5.5. Генерационно-рекомбинационный шум

5.5.1. Генерационный шум обедненного слоя

Существенная часть низкочастотного шума кремниевых ПТ обусловлена флуктуациями зарядовых состояний ХШР-цент-ров, расположенных в обедненных слоях переходов канал - затвор. Кроме того, наличие таких центров определяет основную часть тока утечки этих переходов.

Первыми, кто обратился к вопросу о генерационном шуме в обедненных слоях переходов ПТ, были Лауритцен и Сах [37],

они же подробно рассмотрели этот вопрос в работах, написанных раздельно [36, 50]. Их модель была подтверждена экспериментальными измерениями шума, выполненными на обычных и легированных золотом кремниевых ПТ при изменении в широком интервале напряжений смещения. Поведение легированных золотом кремниевых ПТ рассматривалось также Фу и Сахом [10] в связи с анализом с помощью эквивалентной цепи с сосредоточенными параметрами генерационно-рекомби-нациопного шума, обусловленного флуктуациями заряда на примесных центрах в обедненных слоях переходов канал - затвор.

Генерационный шум в обедненном слое возникает за счет того, чтО каждый из ХШР-центров испускает попеременно то дырку, то электрон, которые удаляются из перехода под действием сильного электрического поля. Такая флуктуация в зарядовом состоянии подобного центра приводит к локальной модуляции ширины обедненного слоя и, следовательно, ширины канала, что в свою очередь приводит к флуктуациям тока, текущего во внешней цепи.

Этот шум можно представить генератором напряжения на входе ПТ, как это показано па рис. 5.4. Эквивалентное шумовое сопротивление такого генератора можно представить в-виде

Рис. 5.4. Эквивалентная схема генератора шумового напряжения в цепи затвора ПТ, характеризующего шум за счет генерации носителей в обедненном слое.

(5.42)

где F{Vg, Vd) - функция, зависящая от значений напряжения

(5.43)

смещения Rn на затворе и стоке, а

T(CpPi+c„ni)-i

- постоянная времени ХШР-центров. Приближение, которое используется в данном случае, соответствует обратно смещенному р-п-переходу. В уравнении (5.43) Ср и с„ - вероятности захвата дырок и электронов, а pi и ni определяются через уровни ловушки Ет собственно уровня Ферми Ei следующим образом [53]:

А = «гехр[(г-£т)/е], (5.44а)

П1 = п.ехр[(£т-£г)/е], (5.44б)

где п/ - концентрация собственных носителей.

Величина Rn сильно зависит от температуры через параметр xt в числителе дроби в уравнении (5.42). Это проще всего показать в случае, когда энергетический уровень ловушки совпадает с собственным уровнем Ферми. В таком случае температурная зависимость xt полностью определяется выражением

Xf ~ tif Q-i ехр {Ево/2Щ,

где Ego - величина запрещенной зоны полупроводника при 6 = 0 К. Множитель е~з/2 в этом выражении оказывает значительно меньшее влияние по сравнению с экспонентой, которая и

1---ПЗК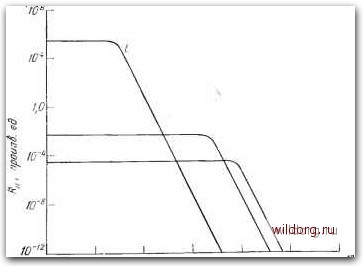

300 к 373Н

10 ~

10 1,0 Частота, Гц

Рис. 5.5. Зависимость R„ от температуры, согласно уравнению (5.42) для кремниевых ПТ.

132 Гшва 5

определяет температурную зависимость п. По мере увеличения температуры величина xt уменьшается и, следовательно, Rn также уменьшается. Такое изменение xt влияет еще и на увеличение частотной полосы Rn при увеличении температуры. Рис. 5.5 иллюстрирует температурную зависимость Rn для случая кремниевого ПТ. Кривые, представленные на этом рисунке, были рассчитаны для значения £go=1,2 эВ, и значения т< = 5 мс при комнатной температуре.

Плотность центров генерации носителей входит в Rn только через масштабный множитель функции F(Vc, Vd). Таким образом, величина шума зависит от концентрации ловушек, но частотная зависимость отсутствует.

Функция F(Vc, Vd) в уравнении (5.42) расходится логарифмически при переходе ПТ в область насыщения. Эта трудность была отмечена Лауритценом [36], который избежал ее в своей двухмерной модели тем, что считал ширину канала у стока конечной и при смыкании. Эта проблема была также рассмотрена Хаслеттом и Трофименковым [20] при анализе, основанном на модели функционирования транзистора в режиме смыкания, предложенной Трофименковым и Нордквистом [59].

5.5.2. Шум канала ПТ

Шум, обусловленный флуктуациями плотности носителей в канале ПТ, был рассчитан ван-дер-Зилом [62], а позднее Влие-том и Хиаттом [69]. Такие флуктуации возможны в тех случаях, когда ХШР- и рекомбинационно-генерационные центры присутствуют в области канала или при низких температурах, если только часть доноров или акцепторов, находящихся в области канала, ионизована.

Спектр такого шума можно выразить через эквивалентное шумовое сопротивление Rn, которое по форме сходно с выражением в уравнении (5.42)

где т - постоянная времени флуктуации. Такая форма спектра экспериментально наблюдалась Хэллдеем и Бранком [14] на кремниевых и германиевых ПТ. Однако трудно определить, был ли шум, который они измеряли, обусловлен флуктуациями плотности носителей в канале или генерационными процессами в обедненной области. В соответствии с работой Саха [50] первая шумовая компонента должна быть незначительной при комнатной температуре.