ную схему, представленную на рис. 4.10, где введен генератор напряжения Теплового шума Vb(t), обусловленного наличием гь. Низкочастотный коэффициент шума транзистора в этом приближении можно получить непосредственно из расчета этой схемы в сочетании с уравнениями (4.92). Считая действитель-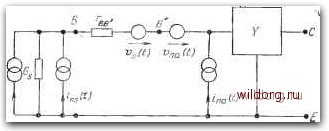

Рис. 4.10. Эквивалентная схема транзистора с учетом сопротивления базы.

ньш полный адмиттанс источника, имеем

где Ге=1/СЕо- Если удовлетворить условиям

Ро > 1 и Гь,

то выражение для коэффициента шума сводится к виду

(r6-fr,/2) , R,

2г,Ро

Теперь запишем его следующим образом:

Rnv i Rs

F~ 1

(4.93) (4.94) (4.95)

(4.96) (4.97а)

7?„, = 2гД. (4.976)

Из этих выражений легко видеть, что Rnv и Rni можно интерпретировать как шумовые сопротивления некоррелированных последовательно соединенных генераторов напряжений и параллельно соединенных генераторов тока на выводах эмиттер - база. Следует отметить, что влияние сопротивления базы на коэффициент шума учитывается просто добавлением сопротивления Гь последовательно к шумовому сопротивлению транзистора.

Rs Rni

.0= V {RnvRnt) = l2/-,Po (/-ь+/-,/2)]1/2, (4.98)

что соответствует минимальному коэффициенту шума

(4.99)

Ясно, что когда Ге>гь, т. е. влияние сопротивления базы пренебрежимо мало, то выражение для минимального коэффициента шума сводится к выражению

f„-l + l/l/p;, (4.100)

что, вообще говоря, и следовало ожидать иа основе уравнений (4.90) и (4.91).

Рабочий диапазон, при котором второе из неравенств (4.94) имеет место, нагляднее всего можно проиллюстрировать на примере, рассмотренном Фолкнером [5]. Напомним, что Ге = = ke/qlc, и, следовательно, когда /с=1 мА, Ге=25 Ом при комнатной температуре. Для малошумящего планарного кремниевого транзистора, который используется для звуковых частот, величина Гь=200 Ом. В этом случае Гегь для величин тока вплоть до /с=125 мкА. При таком рабочем токе параллельное и последовательное шумовые сопротивления в выражениях (4.97) i?„„ = 300 Ом (при Ро=100), i?„/=40 кОм, что приводит на основе уравнения (4.98) к оптимальному сопротивлению источника i?so = 3,5 кОм [уравнение (4.98)]. Соответствующее минимальное значение коэффициента шума на основе уравнения (4.99) составляет Ро(0,%Ъ дБ.

Улучшения величины Fa можно достичь, если уменьшить /с на порядок и более, в этом случае гь в уравнении (4.99) становится значительно меньше члена Ге/2 и минимальное значение коэффициента шума рассчитывается по формуле (4.100). Считая опять Ро=100, получим, что в этом случае £о-0,43 дБ.

Интересная особенность проведенного выше анализа шумовых свойств в области низких частот была отмечена Фолкнером [5]. Он обратил внимание на то, что входное сопротивление на низких частотах в схеме с общим эмиттером {гь + hfeore) примерно такое же, что и подключенное параллельно шумовое сопротивление Rni, так как hfeo обычно находится в интервале Ро-2ро- Это означает, что биполярный транзистор в схеме с общим эмиттером не обладает хорошим коэффициентом шума, если схему не использовать как усилитель напряжения, т. е. пока его входное сопротивление не будет существенно боль-

Условия согласования шума реализуются в том случае, когда сопротивление источника имеет оптимальную величину, описываемую выражением

4.8. Вопросы, связанные

с малым сопротивлением источника

В соответствии с уравнениями (4.94) и (4.98) оптимальным сопротивлением источника можно считать такое, которое имеет минимальное значение для определенных значений Ро и гь, когда Ге = гь. Таким образом, минимальным значением сопротивления оптимального источника является величина гьУЗРо, которая при Ро=100 и гь=200 Ом составляет 3,5 кОм; так как обычно величина Гь крайне редко бывает во много раз меньше 100 Ом, следует ожидать, что оптимальное сопротивление источника будет всегда больше примерно 2 кОм.

В источниках, сопротивление которых менее 2 кОм, возникают проблемы: в этих случаях отсутствует возможность непосредственно удовлетворить условиям для получения минимального коэффициента шума. Одно из решений проблемы в

шим, чем содротивление источника. Это противоречит сложившемуся мнению, неоднократно высказывавшемуся и в литературе о том, чтЬ биполярный транзистор является главным образом усилителе"м тока, и которое, как отмечает Фолкнер, ведет к большому непониманию.

4.7. Вклад 1 -шума в коэффициент шума

Рассмотрение, проведенное выше, абсолютно не затрагивало вопроса о влиянии шума 1/f на коэффициент шума биполярных транзисторов. Фолкнер [5] показал, что этот фактор можно учесть просто, если во все уравнения разд. 4.6 вместо Ро подставить эффективный коэффициент усиления по току ро, который определяют следующим соотношением:

Ро=7Г+. (4.101)

где (Of - характерная угловая частота шума 1/f. Для достаточно хорошего малошумящего кремниевого планарного транзистора значение (йр/2п менее примерно 1 кГц [6]. Для гораздо больших частот ро=Ро, так что можно использовать все выражения, которые проводились выше для расчета коэффициента шума. Когда ш<С<ор, шум 1/f представляет собой существенный вклад в общий шум транзисторов, тогда величина ро-1 и в этом случае подобный элемент уже нельзя считать малошумя-щим. Проведенный выше анализ, очевидно, неприменим в этом диапазоне частот.