где У -параметры, соответствующие элементам матрицы проводимости в уравнении (4.83). Из уравнений (4.64), (4.72) и (4.74) следует, что спектральные плотности этих двух генераторов имеют вид

S,,(«)"29/c/GV

S,„(«)29/b = --/cCoV,

(4.85а) (4.856)

а кросс-спектральная плотность с учетом корреляции между ними описывается выражением

(4.85в)

где Geo - низкочастотное значение проводимости эмиттер - база. При выводе уравнений (4.85) использовались следующие соотношения:

,1. Л%о»Ро»1. «V«1-

(4.86)

После этого коэффициент шума собственно транзистора можно определить, используя эквивалентную схему, изображен-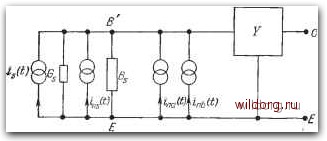

Рис. 4.9. Эквивалентная схема для расчета коэффициента шума транзистора.

ную на рис. 4.9. В ней (О - сигнальный генератор тока; Ys = = Gs+jBs - полный адмиттанс источника сигнала; ins(t) - генератор шумового тока, спектральная плотность которого равна 4kQGs. а 1„ь(О-генератор тока, эквивалентный генератору Vna(t), представленному на рис. 4.8. Согласно теореме Нортро-на, для этого генератора в терминологии преобразования имеем

Inb = ysVna- (4.87)

Из эквивалентной схемы рис. 4.9 и уравнений (4.85) следует.

1 , Gl . 2G,

Ро (Рео GEohfeo]

1ЛН0Г0 квад

f=i+Sfc[(+4S+4/+

(4.88а)

которую при дополнении до полного квадрата можно представить в виде

1 , 0,2 , 2G,

£0 GEhfeo

(4.886)

Штрихи в этих уравнениях указывают, что они относятся к транзистору, включенному в эквивалентную схему.

Оптимальные шумовые условия достигаются тогда, когда реактивная проводимость источника принимает значение

Bso=---GeoC>Tj, (4.89а)

которое соответствует индуктивности источника 3/(2Geo(b4/). Если подставить вместо Bs в уравнение (4.886), то условие согласования шумов определяется минимизацией коэффициента шума по проводимости источника. Эта процедура приводит к оптимальной проводимости источника, описываемой формулой

G30 = G (-4-4 <\У\ (4.896)

откуда следует, что наименьшее значение коэффициента шума имеет вид

где членом, содержащим Ifihfeo, пренебрегли и использовали соотношение Gjso-qlclkQ. Следует отметить, что, как и в эксперименте, согласно уравнению (4.90), минимальное значение коэффициента шума возрастает с увеличением частоты.

Уравнение (4.90) дает представление о предельных значениях шумовых характеристик транзисторов. На низких частотах, когда зависящий от частоты член пренебрежимо мал, Fff сводится к l + l/y, что при Ро=100 соответствует 0,4 дБ. Такая величина находится в хорошем соответствии с измерениями Фолкнера и Хардинга [6], свидетельствующими о том, что шумовые параметры современных кремниевых планарных транзисторов почти достигли своего оптимума и что эффекты,

ЧТО коэффициент шума описывается формулой

-+[(+4+4/)+

(со) 2qlclGEo 2ШС,„ (4.92а)

STTPy - 2(7/е 2/ee/3oG£o, (4.926)

Г,,О, (4.92В)

где Гр,- - нормализованная кросс-спектральная плотность между /ЭННЫМИ генераторами.

Здесь как раз удобное место для введения в рассмотрение сопротивления базы транзистора; оно включается в эквивалент-

обусловленные ненулевым сопротивлением базы и избыточными шумами, т. е. те факторы, которые не рассматривались в проведенном выше анализе, могут быть сведены к пренебрежимо малым значениям.

Когда же по каким-либо причинам адмиттанс источника должен учитываться, то условия оптимального согласования являются невыполненными, т. е. не имеется возможности нейтрализовать индуктивную часть зависящей от частоты составляющей в выражении для коэффициента шума. В этом случае считают Bs=Qi и минимизируют выражение для F в выражении (4.886) относительно Gs, причем минимальная величина коэффициента шума при таких условиях описывается формулой

Очевидно, что это выражение отличается от выражения (4.90) только на высоких частотах, т. е. в тех случаях, когда член, зависящий от частоты, является существенным. Как и в случае уравнения (4.90), данное уравнение представляет собой некий предел для шумовых параметров транзистора, реально не достижимый на практике, так как при выводе его не учитывались эффекты, связанные с конечным сопротивлением базы и избыточные шумы транзистора.

4.6. Низкочастотная эквивалентная схема с учетом сопротивления базы

Эквивалентная схема, представленная на рис. 4.8, точно описывает шумовые свойства собственно транзисторов в достаточно широком диапазоне частот, однако во многих практических случаях она является достаточно сложной. Для частот, значительно меньших величины 1/(Г/"1/ро), эту схему можно упростить, если считать, что генераторы тока и напряжения на рис. 4.8 являются «белыми» и некоррелированными, т. е. [сравни с уравнениями (4.85а) и (4.856)