та событий, fl - значение среднего квадрата амплитуд импульса, а черта над левой частью выражения означает усреднение для большого числа испытаний (т. е. среднее по множеству) .

В особом случае, когда составляющие последовательности импульсов чрезвычайно малы, функция формы отдельного выброса представляется импульсом бесконечно малой ширины. Последовательность случайных импульсов в этом случае считается импульсным процессом [2]. Поскольку фурье-преобразо-вание одного импульса равно единице, из уравнения (1.2) имеем спектральную плотность импульсного процесса:

S7H = 2v. (1.3)

Это важный результат, показывающий, что спектр импульсного процесса постоянен для всех частот вплоть до неограниченно высоких. Такой спектр иногда называют «белым».

Импульсы, возникающие в результате дискретных событий, вызывающих тепловой и дробовой шум, имеют постоянные (равномерные) спектральные плотности до очень высоких частот («очень высокие» означают величины, сравнимые с величинами, обратными фактической ширине импульса). Уровень спектральной плотности в обоих случаях, т. е, значение правой части уравнения (1.3), определяется из рассмотрения физики механизмов шума.

В случае теплового шума вывод основывается на положениях статистической механики и закона равномерного распределения энергии, согласно которому любая система при абсолютной температуре 6, находящаяся в тепловом равновесии с окружающей средой, обладает тепловой энергией в среднем до 9 на каждую степень свободы, где k - постоянная Больцмана. В результате спектральная плотность шумового напряжения на концах сопротивления в разомкнутом контуре имеет вид

5Л«)) = 4А«. (1.4а)

Таким образом, активное сопротивление может быть представлено так, как показано на рис. 1.3, а, где последовательный шумовой генератор напряжения имеет спектральную плотность, описываемую выражением (1.4а). После простого преобразования контура шумовое сопротивление можно представить в виде, изображенном на рис. 1.3,6, где параллельный шумовой генератор тока имеет спектральную плотность

Sj((o) = 4AeG. (1.46)

В этом выражении проводимость G=l/R.

Рис. 1.3. Тепловой шум в резисторе R, представленный последовательный шумовым генератором напряжения (а) и параллельным шумовым генератором тока (б).

Выражения (1.4) были впервые выведены Найквистом [4 из соображений термодинамики и обмена энергией между активными элементами в равновесии. Макроскопический подход Найквиста к проблеме теплового шума, который существенно отличается от исследования на микроскопическом уровне, проведенного выше, описан в приложении 2.

В теореме Найквиста, выраженной соотношениями (1.4а) и (1.46), содержится сопротивление R. Однако максимально возможная мощность на сопротивлении в интервале частот df не зависит от R. Это можно видеть из рис. 1.4, который показывает, что к сопротивлению R, параллельному шумовому генератору тока, подключена бесшумовая согласованная нагрузка. Простой анализ контура показывает, что рассеянная в нагрузке мощность в диапазоне частот df имеет вид

(1.4в)

где вместо Si{w) подставили выражение из правой части формулы (1.46). Значение постоянной Больцмана = 1,38Х X10-23 Дж/К, которая при умножении на величину 6 = 293 К, соответствующую комнатной температуре, в интервале частот шириной 1 Гц дает максимально возможную мощность шума, равную 4-10-21 Вт.

Спектральная плотность дробового шума при среднем токе / составляет

5г(со) = 2/,

(1.5)

где q - абсолютное значение заряда электрона. Этот результат почти непосредственно следует из выражения (1-3), если предположить, что среднее число импульсов в единицу врени равно I/q, а все амплитуды импульсов равны q, что дает a=q.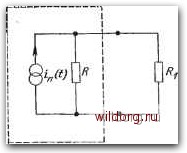

Рис. 1.4. Шумовое сопротивление R, соединенное с бесшумовой согласованной нагрузкой Ri.

\ Изучение теплового и дробового шума на микроскопическом уровне, оёнованное на концепции последовательности случайных импульсов, в дальнейшем несколько подробнее обсуждается в гл. 2.

Один вцд шума, который встречается в самых разнообразных системах (электронных, биологических, музыкальных и т. д.), и особенно в устройствах на твердом теле, приобрел широкую известность. Это является следствием его повсеместного распространения и одновременно сложности для теоретического изучения. Мы имеем в виду 1 -шум, или, как его иногда называют (исторически), токовый шум, фликкер-шум, шум контактов или избыточный шум.

Название 1/f связано с тем, что спектральная плотность энергии этого шума изменяется в зависимости от частоты как /-", где значение а обычно колеблется в пределах 0,8-1,2. Эту зависимость наблюдают при понижении частоты до значений порядка 10- Гц. Верхний ее предел установить трудно, так как он, как правило, маскируется тепловым или каким-либо другим шумом. Существуют различные теоретические трудности при исследовании 1 -шума, главным образом касающиеся сходимости интегралов. В настоящее время не существует ни одного вполне удовлетворительного объяснения этого явления, хотя в некоторых случаях (например, при захвате электронов оксидным слоем на полупроводнике, как это происходит в МОП-полевых транзисторах) модели были получены. Похоже, однако, что такие модели имеют лишь ограниченное применение и не объясняют адекватно многие формы сигналов 1 -шума.

Интересно отметить, что 1 -шум можно представить как последовательность случайных импульсов, или, более точно, последовательность случайных импульсов с определенным видом функции формы импульса, для которой спектральная плотность изменяется как в широком частотном диапазоне. Чтобы

это выполнялось, форма импульса должна иметь вид

f{t)==t-yu{t), (1.6)

как было предложено Шенфельдом [6] и рассматривалось сравнительно недавно ван-дер-Зилом [8]. В выражении (1.6) 4{t)-единичная ступенчатая функция, равная единице для t>0 и нулю, когда <0. Преобразование Фурье для f(t) су-