ЯВЛЯЮТСЯ независимыми. При получении уравнений (4.19) мь1 использовали среднее число случаев в секунду как pAAxfxf, а из уравнения (2.57)-условие D = \x.kQlq=lfl2xf. Интегрируя ;эти уравнения, получим выражения

ki + i

: (4.20a)

ky + h

(4.205)

для спектра флуктуации тока на границе, обусловленных всеми •событиями в п-области.

Сейчас мы не будем давать оценки интегралам в уравнениях (4.20), но через некоторое время мы возвратимся к ним при рассмотрении полных шумов в идеальном диоде. Однако важность этих двух выражений следует иметь в виду.

Из уравнения (4.16) легко видеть, что скорее тепловое движение, а не флуктуации в концентрации носителей вызывает ток через материал. Наряду с этим, очевидно, можно сказать, что имеют место флуктуации и разности Ap(t) концентраций носителей в плоскостях х=х и х=х+Ах, для которых из выражений (4.13) и (4.16) имеем

Др«(Уи) =

DHf AD

(4.21)

при Ax, стремящемся к нулю.

Похожая, но не идентичная уравнению (4.21) формула была выведена ван-дер-Зилом [22] из рассмотрения, основанного на использовании аналогии с передающей линией. В его рассмотрении в левой части соответствующего уравнения находилось значение среднего квадрата (которое было выражено через преобразование) самой концентрации носителей в плоскости х=х\ Согласовать формулировки ван-дер-Зила и анализ, основанный на рассмотрении процессов диффузии, трудно, так как из последнего следует, что среднеквадратичные флуктуации в концентрации неосновных носителей в любой точке п-области можно получить, только проводя интегрирование по всей этой области и учитывая граничные условия при х=0 и x=W. Результатом же такого интегрирования является функция от W и 1юнцентраций на границах ро и pw, которые не входят в правую часть уравнения (4.21).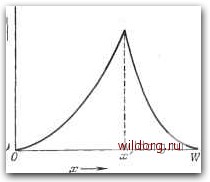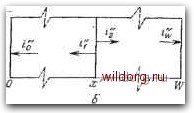

Рис. 4.4.

a - отклонение от равновесной концентрации неосновных носителей, обусловленное актом рекомбинации в плоскости х=х; б - соответствующие релаксационные токи.

h" (М = Ak (/«) р" (/(0), (4.226)

где р" - избыточная концентрация дырок в точке х=х. Как и уравнения (4.13), эти

выражения получаются из зависимого от времени уравнения диффузии. Поскольку накапливание заряда в материале невозможно, то должно выполняться условие непрерывности тока в точке х=х, которое требует, чтобы

tY(/(o) i/(/(o)+9 = 0. (4.23)

Найденная из приведенных выше трех уравнений избыточная концентрация дырок при х=х описывается формулой

p"{j(i>)q/Aiki+k, (4.24)

и Применяя метод, аналогичный использованному при получении уравнения (4.17), имеем для потока неосновных носителей

4.2.2. Генерационно-рекомбинационный шум в объемной области

При акте рекомбинации или генерации не возникает изменения в общем распределении заряда и, следовательно, отсутствует релаксационный процесс основных носителей. Однако имеет место возмущение в распределении неосновных носителей, которое рассасывается потоками неосновных носителей, направленных от места возмущения. Р

Возмущение, или начальное действие, - это мгновенное появление (или исчезновение) неосновного носителя, которое эквивалентно потоку qb (t) «ниоткуда» в плоскости х. Это вызывает отклонение от невозмущенного распределения дырок, как это показано на рис. 4.4, а для случая генерации дырки. На рис. 4.4, б представлены токи неосновных носителей il" и 12", которые как результат начального действия текут к границам х = 0 и x=W соответственно. Эти токи имеют вид

il" iM = ~Ak ijai) p" (/Ю) (4.22a)

через границы

to" (/«) = -Ао(/«)Р" (/«) = •

9 л+й,

(4.25а)

i"\v (/«>) = -117 (/йз) р" (/оз) = •

h + h

(4.256)

Как и в уравнениях (4.17), знаки в уравнениях (4.25) выбира-лотся, исходя из условия, что токи, текущие в п-о6ласти, являются положительными.

Если тд - время жизни неосновных носителей в п-о6ласти, то число случаев рекомбинации за секунду в элементе объема ЛЬ.х составляет pAAx/xR, а число случаев генерации за то же время - РпААх/xr, которое конечно равно скорости рекомби--нации, когда р принимает равновесное значение рп- Когда эти скорости рекомбинации и генерации и уравнения (4.25) подставляются в уравнение Карсона, можно получить спектраль-лые плотности шумовых токов на границах элемента длиной Ах

2 (Р + Рп) qA

2(p + Pn)q"A

h + h

Ax, Ax.

(4.26a) (4.266)

Полную величину рекомбинационно-генерационного шума получают интегрированием этих выражений по всей области

S%)=4\iP+Pn)\

S",v((o) =

ki + k.

(4.27a)

f(P + Pn)

(4.276)

4.2.3. Полный шум перехода

Спектральные плотности полного шума на границах идеального диода представляют собой суммы выражений (4.20) и =(4.27)

SM = SM+S"M,

Sj(co) = Siv(co)+S"jv((o).

(4.28а) (4.286)

Непосредственное суммирование спектральных плотностей в этом случае возможно, так как тепловые токи и токи, обуслов-