Рис. 1.1. Четырехполюсник с шумом (а) и две эквивалентные схемы, в кото» рых шум представлен генераторами тока иа входе ц выходе (б) и генераторами напряжения на входе и выходе (в).

Шумы в электронных схемах обычно рассматриваются как вредный фактор, и, действительно, они часто накладывают огра* ничения на работу устройств. Это справедливо, например, в случае малошумящего усилителя звуковой частоты, в котором минимальная обнаруживаемая мощность входного сигнала зависит главным образом от уровня шумов входного каскада. Однако шум не всегда нежелателен. Известны ситуации, когда присущий системе шум можно использовать как средство для исследования электрических характеристик самой системы. Это может быть в случае, когда, например, требуется измерить проводимость ионного раствора. Обычно такое измерение необходимо проводить, помещая кювету с раствором в электрическое поле. Трудность заключается в том, что при некоторых условиях под действием поля может возникнуть диссоциация молекул, которая в свою очередь влияет на проводимость. Другой способ заключается в измерении шума на клеммах кюветы с образцом в состоянии равновесия (т. е. в отсутствие электрического поля), по величине которого можно судить о проводимости.

Возможно, что двумя наиболее часто встречающимися разновидностями шумов являются тепловой и дробовой. Тепловой шум возникает вследствие случайных флуктуации скорости носителей заряда [электронов и (или) дырок] в резистивном ма-

териале. Этот механизм иногда относят к броуновскому движению носителей заряда, обусловленному тепловой энергией в материале. Тепловой шум присутствует в системе, когда резистив-ный элемент находится в тепловом равновесии с окружающей средой, и часто при первом рассмотрении его отождествляют с шумом Джонсона>) [3]. Флуктуации теплового характера можно рассматривать как механизм, с помощью которого сохраняется тепловое равновесие: за случайным (микроскопическим) отклонением от этого состояния следует, в среднем, возвращение к нему, и очень большое число таких микроскопических «событий» ведет к резкому изменению тока или флуктуациям напряжения на клеммах. Согласно этой точке зрения, форма сигнала тока или напряжения теплового шума должна состоять из очень большого числа отдельных импульсов, связанных с дискретными «событиями», происходящими в резистивной материале.

Дробовой шум связан с прохождением тока через барьер, и в этом смысле он является неравновесной разновидностью шума. Впервые он был рассмотрен Шотки [7], который использовал аналогию мелкой дроби, сыплющейся в контейнер. Дробовой шум или по крайней мере шум, похожий на дробовой, часто встречается в твердотельных устройствах каждый раз, когда ток проходит через потенциальный барьер (например, в обедненном слое р-п-контакта). Детали физического механизма, лежащего в основе дробового шума, будут рассмотрены ниже. Природу дробового шума, возможно, легче понять, если исследовать термоэлектронный диод, в котором Злектроны эмитируют из катода случайным образом и затем перемещаются к аноду под действием электрического поля. Ток, создаваемый этим потоком электронов, флуктуирует случайно около среднего уровня, причем эти флуктуации (т. е. дробовой шум) возникают благодаря случайной дискретной природе эмиссии.

Очевидно, что физическая природа теплового и дробового шума различна, но структура шумовых сигналов обоих типов похожа: оба сигнала можно представить как последовательность случайных импульсов, похожих по форме и случайно распределенных во времени. Пример такой последовательности импульсов, спадающих по экспоненте, представлен на рис. 1.2. В контексте данной книги термин «случайные» означает, что дискретные события, создающие импульсы, независимы и статистический закон, описывающий распределение этих событий во времени, - это функция плотности вероятности Пуассона.

> Неравновесная разновидность теплового шума, связанная с популяциями горячих электронов, наблюдается в некоторых высокочастотных устройствах, которые будут рассмотрены позже. Пока не будет специально оговорено, термины «тепловой шум» и «джонсоновский шум» будут употребляться здесь в связи с равновесным состоянием.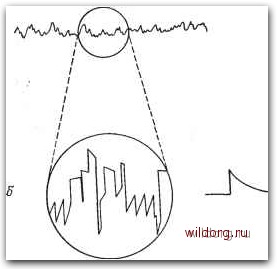

Форма импульса

Рис. 1.2. Схематическая иллюстрация случайной последовательности импульсов (а) и часть сигнала, сильно увеличенная, чтобы показать эффект наложения отдельных импульсов (б).

Распределение Пуассона и условия, при которых оно имеет место, обсуждаются в приложении 1.

Если форма шумового сигнала описывается функцией x{t), а форма отдельного импульса - функцией f{t) [/(0=0 Для <;0 в предположении, что событие, вызывающее появление импульса, происходит при =0 и система причинна], то случайная последовательность импульсов есть линейная суперпозиция

x{f)aj{t-t\ (1.1)

где uk - амплитуда k-то импульса в этой последовательности, а tk - момент времени, в который происходит А-е событие. Распределение tk подчиняется закону Пуассона. Форма шумового сигнала, описываемая выражением (1.1), обладает некоторыми интересными свойствами, подробно рассматриваемыми в гл. 2. В частности, спектральную плотность можно представить в виде

S,(co) = 2vaF(/co)p.

(1.2)

Это утверждение известно как теорема Карсона [5]. В выражении (1.2) ICO - угловая частота, F{ja)-преобразование Фурье функции f{t) формы отдельного импульса, v - средняя часто-