Давно известно, что четырехполюсник с шумом можно представить множеством эквивалентных схем, различающихся лишь расположением шумовых генераторов на входе и выходе бесшумовой схемы. На рис. 2 в работе Монтгомери [7] показаны, например, три различных варианта включения генераторов шума на входе и выходе.

С точки зрения вычисления коэффициента шума схемы особенно интересен эквивалентный контур, в котором оба генератора относятся к входу. Бекинг и др. [1] установили эквива-

Рис 3.3. Схематическое изображение бесшумового четырехполюсника с обозначением токов и напряжений на входе и выходе.

лентность такой конфигурации тем вариантам, в которых шумовые генераторы находятся и на входе, и на выходе; эти авторы показали также, что для полного описания свойств шума четырехполюсника на фиксированной частоте достаточно четырех величин, а именно: спектральных плотностей двух генераторов шума, действительных и мнимых частей взаимной спектральной плотности. Эти четыре величины можно определить по измерениям на клеммах схемы, и таким образом можно получить полное описание характеристик шума четырехполюсника, ничего не зная о структуре схемы или о скрытых физических механизмах, ответственных за возникновение шума. При разработке схемы этого достаточно, но если нужно исследовать связь между структурой устройства и шумом на клеммах, необходимо использовать другой подход.

Токи и напряжения на клеммах четырехполюсника связаны между собой парой линейных уравнений. Для бесшумового четырехполюсника), т. е. не содержащего внутренних источников шума, эти уравнения можно записать через матрицу импедан-

) Такая схема нереальна, так как в действительности все схемы производят некоторый шум. Однако, когда уровень сигнала достаточно высок, влияние шума пренебрежимо мало и уравнения (3.8) справедливы.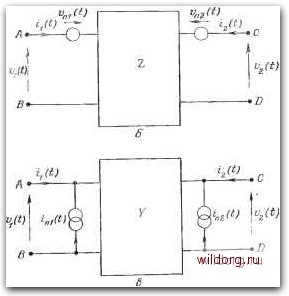

Рис. 3.4. Линейный четырехполюсник с внутренними генераторами шума (а) и его эквивалентная схема по Тевенину с внешними последовательными шумовыми генераторами напряжения (б). Другая разновидность эквивалентной схемы (б)-с внешними параллельными шумовыми генераторами тока (в).

сов схемы Z или через матрицу проводимостей Y следующим образом:

11 = ад+ад. 12 = ад+2:2Л, (3.8а)

/х = ад+ад. /. = ад+ад. (3.86)

Заглавные буквы I м V в этих уравнениях означают фурье-преобразования или фурье-амплитуды в зависимости от того, периодические или апериодические сигналы имеются на клеммах. Индексы 1 и 2 относятся к входным и выходным величинам соответственно, а правило знаков, использованное при составле-

НИИ уравнений, таково, что токи, входящие в систему, положительны, как иллюстрируется на рис. 3.3. Следует заметить, что, вообще говоря, все величины в уравнениях (3.8) зависят от частоты. "Ч

Если четырехполюсник не является бесшумовым, а содержит внутренние шумовые генераторы, иными словами, если уровень шума на клеммах сравним с уровнем сигнала, уравнения (3.8) должны быть перестроены с учетом случайных флуктуации на клеммах. При этом используется известный ныне метод представления четырехполюсника с шумом (рис. 3.4, а) в виде бесшумовой схемы с вынесенными наружу шумовыми генераторами. Применяя теорему Тевенина, можно получить эквивалентную схему, изображенную на рис. 3.4,6, в которой на входе и выходе появляются последовательные генераторы напряжения. Вообще говоря, между этими генераторами возможна некоторая степень корреляции, так как шумовые флуктуации на входе и выходе могут иметь в своей основе, по крайней мере частично, один и тот же физический механизм. Разновидностью схемы на рнс. 3.4, б служит эквивалентная схема, показанная на на рис. 3.4, в, в которой внутренний шум представлен генераторами тока, включенными параллельно входу и выходу. Эти два генератора также могут, вообще говоря, обнаруживать некоторую степень корреляции

При учете вклада от включения последовательных шумовых генераторов напряжения, показанных на рис. 3.4, б, вместо уравнений (3.8а) имеем соотношения между током и напряжением в виде

Vi = ZiJi+ZiJ,-V,i, V=Z,Ji+Z,,Ii-V,„ (3.9а)

и аналогично, когда учитывается вклад от включения параллельных генераторов тока, показанных на рис. 3.4, в, уравнения (3.86) переходят в

/i = niVx+-4i. 4 = ад+ад-п2. (3.96)

Члены, описывающие шум в уравнениях (3.9), представляют собой фурье-преобразования случайных временных последовательностей, КЗ которых состоят шумовые флуктуации тока или напряжения на входе и выходе. Вопрос о существовании таких преобразований обсуждался в предыдущей главе (разд. 2.3 и 2.5). Там пришли к заключению, что хотя инте тральные преобразования в неограниченном интервале не сходятся, в конечном интервале все же допустимо строить собственные спектры и взаимные спектры стационарных временных последовательностей величин при условии, что процедуры усреднения по ансамблю и по времени выполняются в надлежащем порядке. Поскольку конечная цель составления уравнений