q (t) - mqHf/L = vqHfH/L, (2.63)

где V - средняя скорость событий и считается, что m=v(. Из формул (2.55) - (2.57) следует, что

q = 2ikQ/R)t. (2.64)

Появление времени t в этом выражении подтверждает, что флуктуации заряда действительно нестационарны. Выражение (2.64) было впервые выведено Эйнштейном.

Сейчас нас интересуют ковариация, автокорреляционная функция и спектральная плотность флуктуации заряда q{t). Сначала вычисляют ковариацию, затем используют выражение (2.61) для определения автокорреляционной функции, а из нее получают спектральную плотность, используя теорему Винера - Хинчина. Эта процедура, в которой различие между функцией ковариации и автокорреляционной функцией не только подчеркивается, но и используется в вычислении спектральной плотности, применима к нестационарным процессам вообще.

ния частицы. Затем он пошел дальше и показал, что диффузия и броуновское движение - по существу одно и то же явление, поскольку они возникают вследствие быстрого молекулярного движения.

Процессом, аналогичным перемещению броуновской частицы, можно считать флуктуации заряда из-за тепловой энергии электронов, переносимой по внешнему контуру резистора. Флуктуации заряда q{t) можно выразить в виде интеграла по (конечному) интервалу [О, t] тока тепловых шумов

q{t)=Ht)dt. (2.62)

Эта формула дает альтернативное определение процесса Винера- Лёви: это интеграл стационарного процесса, имеющего равномерную, или «белую», спектральную плотность. Хотя интегралы стационарных процессов нестационарны, они тем не менее являются небольшим классом процессов и не представляют нестационарные процессы в целом.

Значение среднего квадрата флуктуации заряда получают на основе простой операции. Снова рассмотрим одномерную модель резистора, описанную в разд. 2.8. Начальная стадия, состоящая из перемещения электрона по пути свободного пролета If между столкновениями,/вызывает во внешнем контуре перенос заряда, равного q{lf/L). Если в момент времени ( имеется т независимых событий, то значение среднего квадрата флуктуации заряда имеет вид

Так как q {t) - кумулятивный процесс, можно написать

q(t-\-x) = q{t)+z{t,x), (2.65)

где z(t, т) -вклад в флуктуации заряда за время между t и {t+%). Так как время корреляции добавочных флуктуации в процессе Винера - Лёви нулевое, два процесса справа в равенстве (2.65) некоррелированы. Отсюда следует, что функция ковариации имеет вид

q(tx)q(t) = qt). (2.66)

Согласно этому, функция ковариации процесса Винера - Лёви не зависит от времени задержки т и равна значению среднего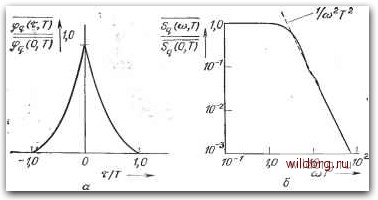

Рис. 2.5. Нормированная автокорреляционная функция {а) и нормированная (односторонняя) спектральная плотность флуктуации заряда в резисторе (б).

квадрата. Таким образом, функция ковариации флуктуации заряда имеет вид

q{t+x)q{t) = 2mtlR. (2.67)

Теперь можно получить автокорреляционную функцию для q{t) из выражения (2.61) r-i-t]

-7- I С 2kQ ,,, kQT ( I т I

фДт,Г)= J -М/ = -1-LL

где Т - время наблюдения процесса q{t). Когда здесь не выполняется неравенство, автокорреляционная функция равна нулю. На рис. 2.5, с показана ф<,(т, Т), нормированная на Ф9(0, Т), в зависимости от xfT.

Выражения (2.67) и (2.68) позволяют провести интересное сравнение: в то время как ковариация не зависит от задержки.

-j, т<Г, (2.68)

автокорреляция явно зависит от т, причем таким образом, что «время корреляции» процесса пропорционально времени наблюдения Т. На первый взгляд, этот результат кажется странным, но его можно понять, если учесть кумулятивный характер процесса; ибо при фиксированном т соответствующая общность между q{t+x) а q{t) в среднем по интервалу [О, Т] возрастает при увеличении времени наблюдения.

Теперь из выражения (2.68) по теореме Винера - Хинчина можно найти спектральную плотность для q{t). Соответствующий интеграл обращения по формуле (2.336) имеет вид

(О), Т) = 4 f ф(т, Т) cos (OTdT, (2.69)

что совместно с выражением (2.68) дает

Эта функция, нормированная к своему значению на нулевой частоте, изображена на рис. 2.5,6 в зависимости от шГ.

Когда <йТ%>1, второй член в квадратных скобках в выражении (2.70) пренебрежимо мал и спектральная плотность изменяется как со~ в соответствии со спектром процесса случайного блуждания, полученного Беллом [2] с использованием метода квадратных разностей. Когда соГ<с1, вырезающее влияние интервала наблюдения изменяет форму спектра, которая в этой области более или менее плоская. Таким образом, оставляя конечным время наблюдения, избегаем тем самым концептуального противоречия с бесконечной энергией на нулевой частоте («инфракрасная» катастрофа), с которой мы встретились бы, если в выражении (2.70) взяли Т бесконечно большим. Так как измерения всегда проводятся в течение конечного времени, это исследование процесса Винера - Лёви должно казаться более реалистичным, чем любой хитроумный способ, в котором допускается, что время наблюдения (в явном или неявном виде) стремится к бесконечности.

2.11. Функция Макдональда

Ковариация нестационарного кумулятивного процесса q(t), определенного в выражении (2.62), может быть выражена в терминах спектральной плотности стационарного процесса i(). Это верно, даже если qOt) не является процессом Винера -Лё-