случае функция H{s) должна быть полосно-пропускающей функцией с достаточно широкой полосой, включающей все основные частотные компоненты сигнала. Ширина полосы сигнала (короткий импульс) велика по сравнению с шириной полосы болванки, так что одна из функций активного фильтра состоит в том, чтобы расширить ширину полосы пропускания всей системы. Здесь существует аналогия с нерезонансным преобразователем, когда активный фильтр расширяет полосу пропускания, чтобы исключить подавление высокочастотных спектральных компонент сигнала.

Для H(s) подходит полосно того порядка

H{s) = -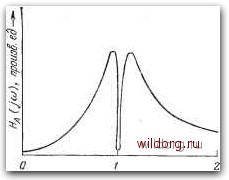

Рис. 13.10. Частотная зависимость модуля передаточной функции Яд(/о)), определяемой уравнением (13.21) при Qm=5,5 и Qb=1000 (эти добротности получены для разрезной болванки).

-пропускающая функция четвер-

(13.20)

где А - постоянный коэффициент; qm<.qb - мера полной полосы пропускания, оптимальную величину которой необходимо определить. Согласно уравнению (13.9), передаточная функция На(5) активного фильтра, которая дает такой полный отклик, определяется отношением H(s)/HB{s)=H{s)ZBis), и, следовательно, из уравнений (13.16) и (13.20) получим

ARbQb + + 0) о

(13.21)

Возможная схема реализации фильтра с такой передаточной функцией предложена Букингемом и Фолкнером [6]. Фильтр имеет глубокий узкий провал на частоте, соответствующей резонансной частоте болванки, как показано на рис. 13.10. Таким образом, шум антенны, сконцентрированный в узкой полосе вблизи частоты ее механического резонанса, сильно подавляется фильтром, а спектральные компоненты относительно широкопо-

лосного сигнала проходят в пределах полосы пропускания фильтра по обе стороны от провала.

Фильтр предназначен для увеличения отношения сигнал - шум на выходе. В оптимальном случае это отношение достигает максимума. Остается определить величину Qm, при которой выполняются эти условия.

13.4.5. Отношение сигнал - шум

Схему системы, приведенную на рис. 13.9, можно представить в другой форме, показанной на рис. 13.11, где H{s) -передаточная функция, описываемая уравнением (13.20). Значе-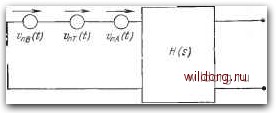

Рис. 13.11. Полная эквивалентная схема детектора.

ние среднего квадрата шума на выходе системы дается интегралом

5.„лИ+"5«„гИ+"5«„лИ \Чт?, (13-22)

где произведена замена s=/a), а спектральные плотности шумов задаются выражениями (13.14), (13.15) и (13.18). После несложных преобразований получаем

Qt=~

2pCrQm

где Qt определяется следующим отношением:

(13.23)

(13.24)

Отметим, что, кроме юо, все величины в этом выражении относятся исключительно к преобразователю и усилителю, а не к болванке.

Хотя вывод о том, что функция H{s) должна быть полосно-пропускающей функцией, основан на характере спектра двойного импульса, имеющего максимальное значение на частоте, от-

Сигнал-шш= -zM- -

un ~ kQe

(13.27)

где для упрощения расчетов используется условие PQt-QbI, применимое как в случае веберовской, так и разрезной болванки. Оптимальный фильтр по определению максимизирует значение этого выражения для величины сигнал - шум по отношению к Qm. При этом легко находится оптимальное значение Qm:

Q„opt = l/3Qr. {13.28а)

откуда следует

(Сигнал-шум)„,„е = (-26)

Соответственно

f kQ \ еЛ/ъ

Минимальная обнаруживаемая энергия = . (13.28в)

Рассматриваемые совместно с выражением для времени разрешения оптимизированной системы, а именно

Дор1 = . (13.29)

ЛИЧНОЙ ОТ нулевой, можно вычислить пиковое значение сигнала на выходе Usp для единичной ступенчатой функции на входе, имеющей величину ступеньки Vm- Импульсная функция отклика системы определяется обратным преобразованием H(s) [уравнение (13.20)], и поэтому отклик на ступеньку определяется обратным преобразованием функции {l/s)H{s). Он представляет собой сигнал, осциллирующий с частотой, равной резонансной частоте болванки, огибающая которого достигает пикового значения через время At=2Qm/(i>o после момента приложения ступенчатого сигнала на входе. Величина этого пикового значения определяется отношением

u,cAvJQe, (13.25)

а соответствующая пиковая энергия, запасенная в болванке,- отношением

W, = §CtvJ/2. (13.26)

Отношение сигнал - шум на выходе равно квадрату пикового значения величины сигнала, деленному на среднеквадратичное значение шума. Учитывая уравнения (13.23), (13.25) и (13.26), оно может быть выражено в виде