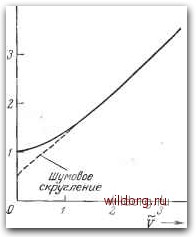тока, протекающего через контакт, можно пренебречь при условии, что туннельный ток мал по сравнению с током, текущим через шунтирующее сопротивление. Тогда единственным значительным источником шума становятся тепловые флуктуации в шунте. Эти флуктуации создают шумовое напряжение на RSJ, если через него протекает постоянный ток источника.

Спектральная плотность флуктуации напряжения на RSJ, через который протекает постоянный ток смешения, была рассчитана теоретически Лихаревым и Семеновым [19], а также Выставкиным с сотр. [27] в предположении, что контакт имеет нулевую емкость и что шунтирующее сопротивление генерирует тепловой шум в классическом пределе, т. е. джозеф-соновская частота удовлетворяет условию hfokQ, где 6 - абсолютная темпертура; h - постоянная Планка; k - постоянная Больцмана. Это ограничение было снято Кохом с сотр. [14], которые показали, что предельный уровень шума при приближении к нулю абсолютной температуры обусловливается нулевыми флуктуациями в шунтирующем сопротивлении.

Подход Коха с сотр. позволяет установить неоднородное нелинейное уравнение Ланжевена для фазы, в котором член, описывающий тепловые флуктуации, входит как часть входного сигнала. В квантовом пределе (т.е. при В = 0) на частоте a)/2jt,. много меньшей, чем джозефсоновская частота, найденная ими спектральная плотность напряжения шумов на RSJ описывается формулой

Рис. 12.5. Вольт-амперная характеристика RSJ в отсутствие шумов (сплошная линия) и в их присутствии (штриховая линия).

S,(o)) = 29OT/K,

(12.20)

где R - шунтирующее сопротивление; Iq - критический ток кон такта; v - среднее напряжение на контакте. Из этой теории также можно получить выражение для спектральной плотности-флуктуации напряжения и при некоторых других ограничениях

Кроме создания шумового напряжения в приборах с джозефсоновскими контактами, тепловые флуктуации приводят к дру тому эффекту: возникновению явления, известного как «шумо

12.5.4. Шум сквидов постоянного тока

Вышеупомянутый теоретический анализ тепловых шумов в RSJ применим и в случае сквида постоянного тока, который в сущности состоит из двух RSJ, включенных в сверхпроводящее кольцо. На основе этой теории Кох с сотр. [16] установили, что предельная чувствительность определяется энергией нулевых флуктуации в сопротивлениях, шунтирующих контакты, и что при оптимальных условиях эти флуктуации приводят к эквивалентной энергии шума, равной Тга. В предположении оптимальной связи с входом, это соответствует шумовой температуре усилителя, приблизительно равной hf/kln2, где f - частота сигнала. Поскольку эта шумовая температура равна предельной величине, устанавливаемой принципом неопределенности, теоретически чувствительность сквида в пределе низких темпратур равна чувствительности идеального линейного усилителя.

В последнее время прилагалось немало усилий, чтобы создать сквид постоянного тока с чувствительностью, приближающейся к теоретическому пределу. Кетчен и Восс [13] создали прибор, работающий при 4,2 К, с энергетической чувствительностью на единицу частоты, составляющей 5 h. Это более чем на порядок лучше того, что было достигнуто в более ранних приборах [5, 8].

вое округление» на вольт-амперной характеристике RSJ. В отсутствие шумов характеристика описывается уравнением (12.11). Вводя нормированное напряжение V=VlhR и нормированный ток Т=1/1о, ее можно записать в следующем виде:

7=(у2+1)1/2. (12.21)

Графическое изображение этой зависимости представлено на рис. 12.5 (сплошная линия). В присутствии шумов вольт-амперная характеристика изменяется, приобретая другую форму, схематично ее вид изображен на том же рисунке штриховой линией. Кох с сотр. провели количественный расчет шумового округления вольт-амперной характеристики при различных условиях, используя численные методы для решения соответствующих нелинейных дифференциальных уравнений. Экспериментальное подтверждение их теории, в том числе и явления шумового сглаживания, было получено недавно при использовании контактов Pb-InOjc-Pb с шунтирующим сопротивлением из CuAl величиной около 0,1 Ом [15].

ЛИТЕРАТУРА

1. V. Ambegaokar, В. I. Halperin (1969), Voltage due to thermal noise in the d. c. Josephson effect, Phys. Rev. Lett, 22, 1364-1366.

2. P. W. Anderson, J. M. Rowell (1963), Probable observation of the Josephsort superconducting tunnelling effect, Phys. Rev. Lett., tO, 230-232.

3. J. Bardeen, L. N. Cooper, J. R. Schrieffer (1957), Theory of superconductivity, Phys. Rev.. 108, 1175-1204.

4. J. Clarke (1973), Low-frequency applications of superconducting quantum interference devices, Proc. IEEE, 61, 8-19.

5. J. Clarke, W. M. Goubau, M. B. Ketchen (1975), Thin film d. c. SQUID with low noise and drift, Appl. Phys. Lett., 27, 155-156.

6. L. N. Cooper (1956), Bound electron pairs in a degenerate Fermi gas, Phys. Rev., 104, 1189-1190.

7. P. K. Hansma, G. I. Rochlin, J. N. Sweet (1971), Externally shunted Joseph-son junctions: generalized weak links, Phys. Rev.. 43, 3003-3014.

8. J. H. Hollenhorst, R. P. Gifford (1979), High sensitivity microwave SQUID,, IEEE Trans. Mag.. MAG-15, 474-477.

9. Yu. M. Ivanchenko, L. A. Zilberman (1968), Destruction of Josephson current by fluctuations, lETP Lett., 8, 113-115. (Originally published ire ZhETF Pis. Red., 8, 189-192, 1968.)

10. R. C. Jaklevic, J. Lambe, A. H. Silver, J. E. Mercereau (1964), Quantum interference effects in Josephson tunnelling, Phys. Rev. Lett., 12, 159- 160.

11. B. D. Josephson (1962), Possible new effects in superconductive tunnelling,, Phys. Lett, 7, 251-253.

12. K. Kanter, F. L. Vernon Jr. (1970), Current noise in Josephson point contacts.. Phys. Rev. Lett. 25, 588-590.

13. M. B. Ketchen, R. F. Voss (1979), An ultra-low-noise tunnel junction d. c. SQUID, Appl. Phys. Lett, 35, 812-815.

14 R. H. Koch, D. J. Van Harlingen, J. Clarke (1980), Quantum-noise theory for the resistively shunted Josephson junction, Phys. Rev. Lett, 45, 2132- 2135.

15. R. H. Koch, D. J. Van Harlingen, J. Clarke (1981a), Quantum noise in Joseph-son junctions and SQUIDs, Proc. of the Sixth Int. Conf. on Noise in Physical Systems, held at the National Bureau of Standards, Gaithersburg, MD, USA, April 6-10 1981, pp. 359-363.

16. R. H. Koch, D. J. Van Harlingen, J. Clarke (1981b), Quantum noise theory for the d. c. SQUID, Appl. Phys. Lett, 38, 380-382.

17. J. Kurkijarvi (1981), Ultimate sensitivity of an a. c. SQUID, Proc. of the Sixth Int. Conf. on Noise in Physical Systems, held at the National Bureau of Standards, Gaithersburg, MD, USA, April 6-10, 1981, pp. 373-375.

18. A. J. Leggett (1981), Quantum tunnelling and noise in SQUIDs Proc. o£

12.5.5. Шум радиочастотных сквидов

Абсолютный предел чувствительности сквида постоянного тока при нулевой температуре устанавливается принципом неопределенности. Абсолютный предел шумового тока, так же как и другие факторы, ограничивающие чувствительность реальных устройств на джозефсоновских контактах, обсуждались Куркиярве [17] и Леггеттом [18]. Они же приводят обширную библиографию последних работ, относящихся к данной проблеме.