С геометрической индуктивностью кольца. В противном случае проблема оказывается более сложной, как отмечается в работах [22, 28].

12.4.1. Сквид постоянного тока

Зависимость тока, протекающего через одиночный джозефсоновский контакт, от магнитного потока представляет собой осциллирующую функцию [23]. Это иллюстрирует рис. 12.3 для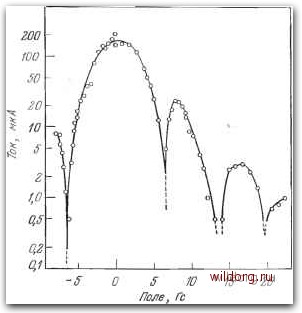

Рис. 12.3. Экспериментальная зависимость тока джозефсоновского контакта от величины магнитного поля ([23], с любезного разрешения Американского физического общества.)

случая Pb-I-Pb-контакта. Минимумы при 6,5; 13,5; 19,5 Гс совершенно отчетливо разделены довольно точно определенными максимумами. Кривая на данном рисунке отображает функциональную зависимость sinx/x, где величина х пропорциональна величине магнитного потока Фо. По форме это аналогично дифракционной картине Фраунгофера, получаемой для света, проходящего через одиночную щель.

Если в сверхпроводящее кольцо включены два джозефсоновских контакта, как показано на рис. 12.2, а, то ток как функция магнитного потока, направленного перпендикулярно плоскости

кольца, также проявляет осциллирующий характер. В этом случае можно провести аналогию с интерференционной картиной, получаемой, когда свет проходит через двойную щель. Теперь наблюдаются две периодичности в зависимости тока от магнитного потока. Одна связана с потоком в единичном контакте,, другая возникает от потока в области между контактами. Такое поведение можно описать, пользуясь понятием критиче-. Г > ского тока /о для двойного контакта. Для него также характерна периодическая зависимость от пронизывающего ф / магнитного потока с периодом, ° равным Фо [10]. Теория сквида была разработана Кларком [4]; ниже приводятся ее основные положения.

В обычных условиях работы через сквид пропускается постоянный ток /, превосходящий более чем в два раза критический ток контактов /о (здесь предполагается, что оба контакта имеют одинаковый критический ток, хотя это не существенно для данного рассмотрения). Тогда на кольце, имеющем по предположению индуктивность L, возникает напряжение 1/>0. Если включается внешний магнитный поток Фе<Фо/2, то должен возникнуть экранирующий ток Is=elL, чтобы поддержать нулевой поток в материале кольца. Когда Ф возрастает до Фе=Фо/2, экранирующий ток: увеличивается до 1а=Фо/2Ь. Если происходит дальнейшее возрастание внешнего потока, то для магнитного потока в кольце-становится энергетически выгодным осуществить переход между квантовыми состояниями (имея в виду квантование потока) таким образом, чтобы экранирующий ток изменил направление. Если Фе=Фо/2+, то экранирующий ток /s=-Фо/21,, а в области Фо/2<ФеЗФо2 величина h возрастает до тех пор, пока в ее верхнем конце h снова не изменит направление, и весь процесс повторится сначала. Функциональная зависимость экранирующего тока от внешнего потока имеет форму зубчатой кривой, изоб-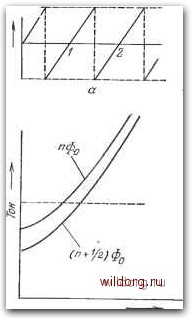

Напряженив S

Рис. 12.4.

с - зависимость экранирующего тока от-величины <I>jii; 6 - вольт-амперная характеристика сквида постоянного тока.

раженной на рис. 12.4, а. Заметим, что скачок возникает, когда Фе=(п+1/2)Фо, где п=0, 1, 2....

Из рис. 12.2, а, очевидно, следует, что если в кольце циркулирует экранирующий ток Is, то суммарные токи, текущие через

контакты, отличаются на 2/; контактов протекает ток /о-2

Поэтому когда через один из Is\, через другой протекает ток

/о. который является критическим для контакта. Следовательно, критический ток сквида постоянного тока Iq на 2l/sl меньше, чем 2/о, т. е.

V = 2/o-2j/J. (12.12)

Этот результат показывает, что критический ток для сквида постоянного тока, как установлено выше, осциллирует при изменении величины приложенного магнитного потока. Максимальное уменьшение величины критического тока, равное Фо/, происходит, когда Фе=(п+1/2) Фо, тогда как минимальное уменьшение равно нулю и происходит при Фе = ПФо.

Вольт-амперные характеристики сквида постоянного тока в этих экстремальных точках приведены на рис. 12.4,6. Если ток смещения / превышает 2/о (как показано на рисунке), то напряжение на интерферометре периодически изменяется с увеличением внешнего потока Фе, причем сигнал имеет треугольную форму. Если каждый из контактов имеет сопротивление R, то глубина модуляции этого напряжения составляет

AF = 2/,Ue4 = T (12.13а)

где 2 [/s] макс = Фс/ -максимальное уменьшение критического тока сквида. Для R=5 Ом, L = 10~s Гн величина V приблизительно равна 5 мкВ.

В случае треугольной формы зависимости изменения напряжения на сквиде от изменения внешнего магнитного потока выражение для вариации напряжения, вызванной малым изменением приложенного потока бФе, имеет вид

6Ус(Я/ЦШ>. (12.136)

При значениях параметров, приведенных выше, это дает .6У/6ФвС5Х109 В/Вб.

В основном сквид используется как нуль-детектор в цепи отрицательной обратной связи: малое изменение величины приложенного потока приводит к изменению напряжения, которое управляет устройством, генерирующим зануляющий ток, представляющий собой сигнал обратной связи в системе. Для сквида, имеющего индуктивность L=10~ Гн, можно достичь разрешения лучше, чем 10~*Фо/УГц, соответствующего изменению напряжения на контакте около 1 нВ/уГц.