Джозефсоновский контакт можно изготовить различными способами. Структура, использованная для первых наблюдений джозефсоновского туннелирования [2], состояла из напыленной на подложку полоски сверхпроводника со слоем окисной пленки толщиной около 10 А, который отделял ее от такой же полоски, напыленной перпендикулярно первой. Позднее были разработаны другие типы туннельных переходов, включая мостики и точечные контакты. Некоторые из этих приборов и их относительные достоинства рассмотрены Кларком [4].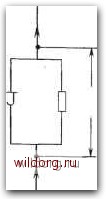

Vo(t)

Рис. 12.1.

а - резистивно-зашунтированный контакт; б - вольт-амперная характеристика (сплошная линия), которая при больших токах асимптотически приближается к прямой RI (штриховая линия).

В общем случае туннельный элемент в реальном джозефсо-новском контакте зашунтирован емкостью, которая приводит к гистерезису вольт-амперной характеристики. Это весьма нежелательное явление в таких устройствах, как сквид, и от него обычно избавляются путем шунтирования контакта подходящим сопротивлением R. Тогда контакт можно представить эквивалентной цепью, изображенной на рис. 12.1, с. Вольт-амперная характеристика резистивно-зашунтированного контакта (RSJ) широко используется в различных расчетах. По этой причине мы остановимся на ней подробнее.

С помощью уравнения (12.4) изменяющееся во времени напряжение Уо на RSJ может быть выражено следующим образом.

(12.6)

где />/о -общий (не зависящий от времени) ток в цепи. Это

уравнение можно решить относительно Ф непосредственным интегрированием

-р=(+«. (12.7)

где 0 - постоянная интегрирования, а а= /о. Интеграл в левой части этого выражения вычисляется хорошо известным методом подстановки «=tg (Ф/2). После нескольких прямых алгебраических преобразований получаем следующий результат:

Ф = 2 tg-i {а-1 [(«2-1)1/2 tg[(а2 1)1/2 (12.8)

где r[ = qRhlb. Анализируя это выражение, можно видеть, что, хотя внутренний тангенс стремится к бесконечности, когда его аргумент равен 2пя/2, производная dOldt (которой мы собственно и интересуемся, так как она дает Fo) непрерывна во времени. Фактически производная dOjdt - периодическая функция с периодом

Г =------. (12.9)

11 (а2-1)1/2 f

Однако осцилляции Fo на этом интервале не являются симметричными, и средняя величина напряжения, определенная за период

о 2q \dl / 2qT J dt - 2qT * (1-iu;

не равна нулю. Определяя границы периода, как два последовательных момента времени, для которых внутренняя функция тангенса в уравнении (12.8) стремится к бесконечности, получаем [Ф(7)-Ф(0)]=2л; и, следовательно,

<F„> = (а- 1)1/2 (/2 /2)l/2 (J2.1 1)

Это уравнение описывает вольт-амперную характеристику RSJ. Отметим, что для токов, протекающих через RSJ, больших по сравнению с критическим током контакта, среднее напряжение асимптотически стремится к величине RI.

Вольт-амперная характеристика, описываемая уравнением (12.11), представлена на рис. 12.1,6. Из ее вида можно заключить, что переменная составляющая сверхтока вносит заметный вклад в усредненный по времени ток через RSJ, даже когда напряжение, меняющееся во времени, достигает такой величины, что ток в несколько раз превосходит критический. Из этого следует, что изменения критического тока могут оказывать влияние

на наклон характеристики в значительной ее части. Измерения вольт-амперных характеристик резистивно зашунтированных контактов показали хорошее согласие с уравнением (12.11) [7].

12.4. Интерферометры Джозефсона

Когда по сверхпроводящему кольцу протекает ток, возникает квантовомеханическое явление, известное под названием квантование потока: магнитный поток в кольце принимает только дис-

Рис. 12.2.

а - сквид постоянного тока, содержащий два джозефсоновских контакта в сверхпроводящем кольце; б - радиочастш ный сквид с одним джозефсоновским контактом в сверхпроводящем кольце, слабо связанным с резонансным колебательным контуром.

кретные значения, кратные по величине кванту потока Фо==/г/29~2-10~ Вб. Это позволяет достичь очень хорошего разрешения в двух типах датчиков магнитного поля, оба являются квантовыми интерферометрическими устройствами (скви-дами). Первым был разработан сквид постоянного тока, состоящий из сверхпроводящего кольца, содержащего два джозефсоновских контакта (рис. 12.2,а), позднее был создан радиочастотный сквид, в котором один контакт включался в сверхпроводящее кольцо, индуктивно связанное с внешним колебательным контуром (рис. 12.2,6).

Поведение обоих типов сквидов можно исследовать на основе простейших теоретических моделей, базирующихся на предположении, что в сверхпроводящем кольце, содержащем один или более джозефсоновских контактов, все равно существует квантование потока. Это предположение неявно подразумевает малость индуктивности контакта или контактов по сравнению