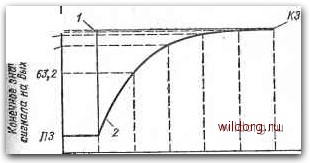JT -fr Я/7еяя

Рис. 3.2. Переходная характеристика линейного преобразователя первого порядка:

ПЗ - первоначальное значение; / - мгновенное изменение измеряемой величины; 2 - конечное значение

между значением в конце предыдущего отрезка и конечным значением. Выходные значения сигнала в процентах конечного значения по проществии каждого отрезка времени продолжительностью в одну постоянную времени приведены в табл. 3.1.

Таблипа 3.1. Переходная характеристика линейного преобразователя первого порядка

Поскольку кривая на рис. 3.2 является экспонентой, это означает, что теоретически выходной сигнал не достигает никогда своего конечного значения. Поскольку по проществии времени, равного 5т, выходное значение сигнала отличается от его конечного значения всего лищь на 1 %, то практически можно считать, что после 5т выходное значение конечно. Безусловно, это всего лищь инженерное приближение, ни больше, ни меньше. Промежуток времени, прошедший между моментами достижения

выходным сигналом соответственно 10 и 90 % его конечного значения, называется временем нарастания.

Важным следствием рассмотрения этой линейной характеристики первого порядка является то, что время срабатывания преобразователя можно в общем случае характеризовать постоянной времени т.

Линейная реакция второго порядка

На рис. 3.3 показана переходная характеристика другого возиможного преобразователя для ступенчатого изменения измеряемой величины. Qna существенно отличается от рассмотренной ранее и свидетельствует о том, что выходное значение сигналаколеблется около конечного значения (с так -называемой кольцевой частотой) прежде чем его достигнуть.

Максимальное значение, на которое выходной сигнал превосходит конечное значение, является выбросом кривой. Максимальное значение выброса имеет пик первого колебания. Если чувствительный элемент преобразовате-

Время

Рис. 3.3. Переходная характеристика линейного преобразователя второго порядка:

2 - мгновенное измеиенне измеряемой величины; 2 -выброс кривой; КЗ - конечное значение

ля работает в режиме свободных колебаний, то его частота называется собственной угловой частотой соп, не обязательно равной кольцевой частоте.

Время, в течение которого выходное значение колеблется вокруг конечного значения либо в течение которого оно вообще колеблется, зависит от демпфирования, прикладываемого к преобразователю. На рис. 3.4 показана переходная характеристика преобразователя для трех

типов демпфирования: недостаточное демпфирование (которое дает такую же переходную характеристику, что и представленная на рис. 3.3); передемпфирование (с переходной характеристикой, которая не колеблется, но имеет значительную постоянную времени установления конечного значения); критическое демпфирование (с переходной характеристикой без колебаний, достигающей конечного значения за кратчайшее время). Несомненно, критическое демпфирование является идеальным для такого преобразователя.

Время

Рис. 3.4. Эффект демпфирования выходной переходной характеристики линейного преобразователя второго порядка:

t - недостаточное демпфирование; 2 - критическое демпфирование; 3 - передемпфирование

Отношение действительного демпфирования к степени демпфирования, необходимого для критического демпфирования, называется отношением демпфирования или коэффициентом демпфирования и обозначается далее в тексте символом Ь. Так, отношение демпфирования, равное 1, означает критическое демпфирование, большее значение отношения соответствует передемпфированию, а меньшее - недостаточному демпфированию.

Преобразователи такого типа называются преобразователями с линейной переходной характеристикой второго порядка. В то время как преобразователи с линейной характеристикой первого порядка могут описываться одной величиной - постоянной времени, дЛя описания преобразователей с линейной характеристикой второго порядка требуются Две величины: отношение демпфирования b и .собственная угловая частота ««.

Несколько сложнее вычислить линейную переходную характеристику второго порядка, не задача упрощвется.