Приведенное распределение интенсивности построено для случая одного прохода плоской электромагнитной волны через активную среду и определяет характеристики скорее усилителя, чем лазера, поскольку в нем не учитываются особенности распределения электромагнитного поля в резонаторе и влияния зеркал. Тем не менее, оно может быть использовано для оценки влияния неоднородности активной среды на расходимость лазерного излучения. Влияние газовой динамики на оптическое качество активной среды газодинамического СОг-лазера с сопловым блоком сотовой конструкции показано на рис. 60.

Сверхзвуковой поток за срезом соплового блока сотовой конструкции имеет оптические неоднородности с характерной ромбовидной структурой скачков уплотнения (рис. 60, о), образующихся при взаимодействии струй, истекающих из индивидуальных сопл (см. рис. 43, 44), и следов, обусловленных стекающими со стекол сопл пограничными слоями. С увеличением расстояния от среза блока уровень оптических нео; нородностей уменьшается, поэтому искажения волновог фронта, прошедшего через активную среду излучения, так» снижаются вниз по потоку (рис. 60, б).

Интересной особенностью регулярных газодинамически структур, образованных мелкомасштабными соплами, явля ется сильная зависимость оптического качества среды от углг наклона оптической оси к оси симметрии блока. При опт» мальных углах наклона, для которых обеспечивается хорошее взаимное перекрытие неоднородностей от соседних сопл диаграмма направленности имеет вид, близкий к дифракционному (рис. 60, в), в то время как для той же активной среды, но ориентированной неоптимально относительно проходящего излучения, расходимость излучения существенно увеличивается (рис. 60, е).

Картина течения активной среды в сверхзвуковом неире; рывном химическом лазере, полученная методом тальбот-иН;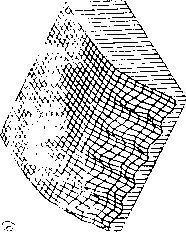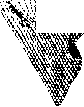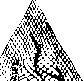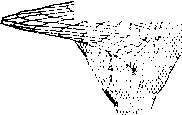

u s X as a. s

терферометрии (рис. 61, а), показывает структуру течения смешивающихся химически реагирующих сверхзвуковых струй. Искажения фазовой поверхности наблюдаются по всей апертуре (рис. 61, б). Тем не менее, распределение нн-

Рис. 61. Йнтерферограмма газодинамического тракта (я) и распределение фазы (б) в выходном сечении непрерывного химического лазера

тенсивности в дальней зоне и в этом случае характеризуется центральным максимумом, в котором сосредоточена основная энергия излучения. Эти результаты получены в предпо-ложени, что размеры активной среды пренебрежимо малы 110 сравнению с расстоянием между плоскостью объекта и плоскостью изображения, т. е. влияние неоднородностей активной среды определяет только начальное распределение фазы электромагнитного излучения в вцходной апертуре лазера, а далее световая волна распространяется в пустом пространстве. Наиболее точно такое предположение соответствует распространению лазерного излучения в вакууме.

4.3, Распространение лазерного излучения в средах

4.3.1. Ослабление лазерного излучения

В пространстве, заполненном газовыми молекулами и конденсированными частицами, будет изменяться пространственное распределение света, по сравнению с рассчитанным по скалярной теории дифракции, и наблюдаться снижение полной мощности распространяющегося излучения.

Для широкого круга практических задач при умеренных плотностях электромагнитной энергии взаимодействие излучения со средой не зависит от интенсивности самого излучения, и все особенности распространения света в различных средах объясняются его ослаблением в результате рассеяния и поглощения. Ослабление излучения в средах рассчитывается законом Бугера, характеризующего свойства среды пропускать излучение. Пропускание излучения D определяется экспонентой

D = exp

J К (2) dz

"о

(4.7)

где - показатель ослабления среды для излучения с длиной волны к, имеющей размерность м-. В общем случае показатель ослабления складывается Из показателей рассеяния яр и поглощения ki„.

В прозрачной однородной среде плоская волна распространяется только в прямом направлении, не испытывая рассеяния в стороны. Например, параллельный пучок света в чистом воздухе или в высококачественном стекле почти не Виден при наблюдении сбоку, т. е. свет почти не рассеива-

ется в стороны. В то же время при наличии в среде части] даже очень мелких, пучок света становится отчетливо виден со всех сторон. Рассеяние света происходит и тогда, когда сами взвешенные частицы имеют размеры, меньшие длины волны, и недоступны прямому наблюдению. Такие среды называют мутными. В соответствии с законом Рэлея интенсивность рассеянного мутной средой света обратно пропорциональна 4-й степени длины волны. Опыт показывает, что рассеяние света происходит не только в мутных средах, но и в среде, тщательно очищенной от посторонних примесей или включений. Причиной этого являются флуктации плотности и, следовательно, показателя преломления, вызываемые хаотическим тепловым движением молекул. Такой тип рассеяния называют молекулярным. Наиболее известный пример - молекулярное рассеяние солнечного света в земной атмосфере, которым объясняется голубой цвет неба. Этот эффект легко наблюдаем благодаря большой толщине рассеивающего слоя газа, в то же время рассеяние в чистом веществе, как правило, очень слабое. Исключение составляет явление резонансной флуоресценции, при котором энергия падающего пучка может почти целиком перейти в энергию рассеянного излучения. Оно наблюдается при совпадении частоты падающего света с собственными частотами частиц среды. Рассеяние света на мельчайших частицах и молекулах, для которого выполняется закон Рэлея, называют рэлеевским рассеянием. Вероятность поглощения фотонов оптического излучения молекулами среды определяется, как известно (см. подразд. 1.1), структурой энергетических молекул и длиной волны излучения. Поэтому молекулярное поглощение очень сильно зависит от конкретных характеристик среды (в первую очередь, ее состава) и спектральных характеристик лазерного излучения.

Влияние состава связано с двумя факторами: 1) с присутствием в среде молекул, энергетические спектры или отдельные спектральные линии которых совпадают со спектром или линией излучения лазера. Только в этом случае, как известно, может происходить поглощение квантов излучения молекулами; 2) с количеством или концентрацией таких молекул в среде.

В более общем виде для всех частиц это положение состоит в том, что показатель ослабления в законе Бугера (4.7) пропорционален концентрации поглощающих частиц n{z) и

сечению ослабления на длине волны X, в расчете на одну частицу 5(2); к),{г)-=п{г)-5к(г). Сечение ослабления Sx (г) определяется как отношение потока поглощаемой частицей энергии к интенсивности падающего на частицу излучения. Эта величина имеет размерность площади. Если в среде находятся частицы, размеры которых сравнимы или превышают длину волны падающего излучения, то взаимодействие излучения с этими частицами не может описываться законом Рэлея.

Теоретическое решение задачи о взаимодействии плоского волнового фронта электромагнитного излучения со сферическими частицами, размеры которых могут быть порядка или больше длины волны, было впервые разработано Дж. Ми в 1908 г. Схематическое изображение процессов, происходящих при взаимодействии света с частицей, представлено на рис.62.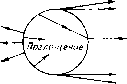

Дифрахциа

Рис, 62. Ослабление излучения частицей

Отраженный дифрагированный и рефрагированный свет "с!ывается рассеянным. Ослабление излучения складывается из рассеяния и поглощения. Закон Бугера для объема с одинаковыми (монодисперсными) частицами (без учета молекулярного ослабления) при концентрации п: Dp = exp(-SxpX Х/гр-2), где S;tp -сечеипе ослабления на частицах.

Для среды, содержащей частицы различных размеров и Переменной концентрации, расчет ослабления существенно Усложняется:

Dp = ехр 9 Зак. W° 43

{\S,{d,)J(z,d,)dzdd, Li, о