Вероятности вынужденных переходов Wmn и Wnm пропорциональны спектральной плотности энергии электромагнитного поля: Wmn = Bmn-pv, Wnm = B„m-pv, ГДС Втп И - КО-

эффициенты Эйнштейна для вынужденного излучения и поглощения соответственно.

В системе из многих частиц в электромагнитном поле могут происходить все три процесса: спонтанное-н индуцированное излучение и поглощение.

В термодинамически равновесных системах полная энергия системы не изменяется, поэтому число переходов т-уп н «-*-m должно совпадать:

пВпт - (Вп г.. f/!„,„) Л„, (1.4)

где iV„ и iVm-число частиц на уровнях « и m соответственно.

При тепловом равновесии распределение частиц по уровням описывается распределением Больцмана

(1.5)

где gt - статистический вес уровня, характеризующий число возможных состояний с энергией е,-. Для простоты изложения будем считать, что рассматриваемая система невырожденная, т. е. ,= 1.

Используя распределение Больцмана, преобразуем выражение (1.4):

. + P)exp(-eJ/;;r) = fi„„ pv ехр(-е„/АГ). (1.6)

При Г-*-оо спектральная плотность энергии неограниченно возрастает и, следовательно, при достаточно высоких температурах Sm„-pv>u4m„, однако при этом экспоненты в формуле (1.6) будут стремиться к единице. Отсюда можно получить первое соотношение между коэффициентами Эйнштейна: Втп = Впт, Т. е. вероятности процессов вынужденных поглощения и излучения равны. Тогда (1.6) можно переписать в виде

(1.7)

Известно, что при достаточно больших XT (или Г/v) спектральная плотность энергии pv должна Определяться формулой Рэлея---Джинса (1.2); Тогда, разложив экспоненту в вы-

ражении (1.7) в ряд и ограничиваясь первым членом разложения, можно получить второе соотношение между коэффициентами Эйнштейна;

AmniB„„ = Shy4c\

(1.8)

Подставляя равенство (1.8) в формулу (1.7), приходим к формуле Планка (см. (1.3)), полученной на основе квантоме-чанических представлений;

Гакой вывод явился первым подтверждением правильности гипотезы Эйнштейна о наличии процессов вынужденного излучения. Именно эта возможность рождения индуцированных квантов света оказывается решающим обстоятельством, приведшим к созданию генераторов направленного монохроматического излучения - лазеров.

В приведенных выше рассуждениях предполагалось, что при квантовых переходах частица излучает или поглощает кванты света строго одной и той же частоты Vmn = {гт-гп)/1г (рис. 4, а). Если бы это было так, то спектры излучения (или поглощения) состояли из бесконечно тонких спектральных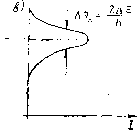

Рис. 4, Ра.змытие энергетических уровней е™ и вп, обуславливающее наблюдаемую ширину спектральной линии

линий. Наблюдаемые же в действительности спектральные 1ИНИИ имеют некоторую ширину (рис. 4, в). Их ширина связана с тем, что уровни энергии частиц в реальных условиях несколько размыты (рис. 4, б) вследствие влияния различных факторов. Даже для изолированной квантовой системы

линии спонтанного излучения имеют конечную ширину. Это так называемая естественная ширина линии является минимально возможной и связана с соотношением неопределенностей, являющимся одним из фундаментальных законов квантовой механики, согласно которому неточность в определении энергии системы и времени ее существования должна удовлетворять соотношению Ае-А>Л/2я, или с учетом определения коэффициента Эйнштейна для спонтанного излучения естественная ширина линии Avo = m„/2n. В оптическом и инфракрасном диапазоне эта ширина, как правило, незначительна.

Реально наблюдаемые уширения спектральных линий связаны, в первую очередь, с процессами возбуждения частиц при столкновениях с другими частицами или со стенками сосуда. Рост ширины спектральной линии в этих случаях называется столкновительным уширением и увеличивается с ростом давления. Кроме того, даже в разреженных газах наблюдаемые линии уширяются из-за эффекта Доплера, вызываемого тепловым движением частиц. В твердых телах уши-рение спектральных линий может быть связано с воздействием электрических и магнитных полей. В общем случае полная ширина линий излучения или поглощения определяется всеми механизмами уширения. Учет реальной формы спектральных линий важен при количественном анализе процессов вынужденного излучения и поглощения.

1.2. Принцип действия лазера

Рассмотрим вещество, в котором имеется достаточное число возбужденных частиц с энергией Вт. Число таких частиц Nm называется населенностью уровня е™. Если населенность уровня Em больше населенности Nn уровня е„, расположенного ниже, т. е. Nm>Nn, то такое вещество называется активным. Если на активное вещество падает электромагнитное излучение, частота которого Vmn, то по мере прохождения электромагнитной волны через вещество будет происходить его усиление благодаря тому, что количество вынужденных переходов атомов с уровня Вт на е„ будет превосходить число актов поглощения е„-ет. Таким образом, квантовое усиление происходит за счет внутренней энергии системы. С точки зрения квантовых представлений, это означает, что пролет квантов (фотонов) через активное вещество вызывает

рождение новых, точно таких же фотонов, t. е. .иррисхйдит явинное «размножение» фотонов.

Чем больше фотонов содержится в электромагнитном из-пучении (т. г. чем выше интенсивность излучения), падаюнгем 1 активное вещество, тем больше вынужденных квантовых "пеходов может произойти. Поскольку скорость нарастания тнтенсивности излучения пропорциональна самой ннтенсив-шсти, то ее изменение

dljdlkj, (1.9)

где fev - коэффициент усиления активной среды. Интегрируя уравнение (1.9), получаем

(1.10)

где / - расстояние, пройденное электромагнитной волной ff активном веществе. Естественно, что возрастание интенсивности излучения в активной среде, описываемое выражением (1.10), не может происходить неограниченно.

В процессе «размножения» фотонов, даже при существовании механизма, обеспечивающего поддержание инверсной часеленности в активной среде, неизбежно наступит момент, когда концентрация фотонов превысит концентрацию возбуж-.енных частиц и прекратится экспоненциальный рост интенсивности излучения. Фактически это будет выражаться в уменьшении коэффициента усиления, начиная с некоторой величины интенсивности излучения, называемой интенсивностью насыщения Коэффициент усиления, характеризую-пшй активную среду при A-cAv и не зависящий от конкретного значения А„ называют коэффицснтом усиления слабого сигнала (или ненасыщенным коэффициентом усиления). Изменение коэффициента усиления от роста интенсивности падающего излучения выражается зависимостью (см. рис. 5):

где км - коэффициент усиления с учетом насыщения.

Однако в естественных условиях для термодинамически равновесных систем населенность энергетических уровней подчиняется известному распределению Больцмана (см. формулу (1.5)), т. е. уровни с меньшей энергией Вп населены больше, чем уровни с большей энергией вт, т. е. Л,„<Л„.При 5ТОМ одновременно с усилением света за счет индуцирован-

ных квантовых переходов, сопровождающихся излучением фотонов, происходит подавляющее ослабление за счет вынужденного резонансного поглощения. Отсюда следует, что для усиления света веществом необходимо искусственно изменить населенности уровней в веществе, а именно: увеличить населенность верхнего уровня и уменьшить - нижнего Nn. Такое активное состояние вещества называется состоянием с инверсной населенностью уровней. Основная трудность в получении инверсной населенности состоит в том, что «антибольцмановское» распределение частиц по анергиям является сильно неравновесным, и его невозможно достичь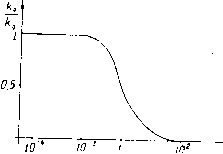

Рис. 5. Зависимость коэффициента уснлення активной с)}еды от интенсивности монохроматического излучения

обычным способом передачи энергии. Инверсную населенность можно формально представить как состояние с отрицательной абсолютной температурой (рис. 6). Действительно, рассматривая отношение населенностей верхнего уровня к нижнему (на каждом из них число частиц связано с температурой и энергией выражением (1.5)), получаем:

= ехр

отсюда

Поскольку ет>е„ и Nm>Nn, то Ттп<0 (см. рис: 6).

Получение «антибольцмановского» распределения не противоречит, однако, третьему началу термодинамики (согласно

которому невозможно достигнуть температуры, равной абсолютному нулю, а тем более низшей) потому, что утверждение это относится к термодинамической температуре, а температура, определенная для населенностей уровней, имеет совершенно другой характер (она называется статистической

0 L<0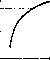

Рнс. 6. Зависимость статистической температуры fmn двухуровневой системы 6т населенностей уровней

температурой или температурой перехода). Для реальных тел можно определить много статистических температур - столько, сколькими способами можно связать в пары его энергетические уровни. Все они равны друг другу и термодинамической температуре тогда и только тогда, когда вещество находится в термодинамически равновесном состоянии, характеризующемся распределением Больцмана.

Необычность инверсной населенности в реальных системах и сложность ее получения надолго отодвинули время практической реализации таких состояний вещества, т. е. создания лазера.

Первые эксперименты были проведены в 1939 г. Советский ученый В. А. Фабрикант наблюдал усиление света, прошед-