ными дифракционной поперечной связью, т. е. вынужденное излучение всех активных частиц будет синхронизовано по фазе и выходной пучок может иметь постоянную по фронту фазу. Излучение, сформированное в таком резонаторе, характеризуется одномодовой структурой.

В резонаторах с Л/ф>1 дифракционными поперечными связями можно пренебречь и, согласно приближенной геометрической оптике, пучки в таком случае могут распространяться по независимым друг от друга замкнутым траекториям, которые могут существовать в активной среде и поддерживаться зеркалами резонатора (рис. 55, б). Отбирая энергию с разных частей активной среды, эти различные поперечные моды генерируют независимо друг от друга и вызывают пространственную некогерентность выходного пучка. Если в резонаторе вблизи оптической оси существует цент-•альная область, радиальный размер которой соответствует ЛФ! и в которой, следовательно, лазерное излучение свя зано дифракцией, то излучение из этой области согласовано по фазе. Однако в неустойчивом резонаторе происходит непрерывное расширение пучка при каждом проходе, поэтому излучение центральной моды, имеющей постоянную фазу, заполняет всю активную среду и, в конечном счете, обтекает одно из зеркал, формируя лазерный луч (рис. 55, в). Таким образом, неустойчивый резонатор можно представить как совокупность одномодового генератора и окружающего его многопроходного усилителя. Так как фаза выходного излучения задается центральной частью резонатора, то в таких резонаторах поддерживается высокое качество выходного излуче- ния.

4.1.3. Энергетическая эффективность резонатора

Энергия и мощность лазерного излучения определяются характеристиками активной среды (коэффициентом усиления, пороговой интенсивностью излучения, населенностью уровней) и параметрами резонатора (оптической схемой, геометрическими размерами, коэффициентом пропускания зеркал, уровнем потерь). Для вычисления мощности стационарной генерации лазера существуют расчетные методы, позволяющие получить численные значения этой величины для различных типов лазеров и конструкций резонаторов. Наиболее общим подходом, позволяющим оценить эффективность работы ре-

"онатора, является определение коэффициента полезного действия резонатора Цр.

КПД резонатора Цр характеризует отношение энергии, выведенной из резонатора Ер, к энергии активной среды Ео, находящейся в резонаторе, которую в принципе можно преобразовать в излучение:

Лр = р/О =• £р/(£а с • % • TIk) ,

где £ас - энергия, затрачиваемая на накачку активной среды. Пренебрегая потерями в активной среде, для оценки Цр можно воспользоваться соотношением: т)р=1-kv/kv, где fev коэффициент усиления слабого сигнала; fev - пороговый коэффициент усиления (см. (1.11)).

Для устойчивого резонатора КПД максимален при оптимальном коэффициенте пропускания выводного зеркала

Topt: Topt = y2a• • L-а, где а -суммарные потери на зеркалах (поглощение). Тогда Лрopt = (1 -ia/2kvL)(1/р/Уас), где lp/ac - отношение объема той части активной среды, которая участвует в усилении света (см. рис. 54), к общему объему активной среды.

Для неустойчивого резонатора максимальная эффективность

1popt = (l-]

может быть получена при коэффициенте увеличения М, где 2\nM = i2akyL~a.

В общем случае баланс энергии в резонаторе с движущейся активной средой характеризуется различными видами Потерь (рис. 56). Энергия излучения может быть представлена как энергия активной среды за вычетом всех потерь энер-i ни в резонаторе:

£"р = £о - ДЕре,, - Af „„„ - ДЕр„ ~ Е, - Д£„.

оль отдельных видов потерь может быть различна в каждом !<онкретном случае. Обычно i}p = £p/£o=0,3... 0,7.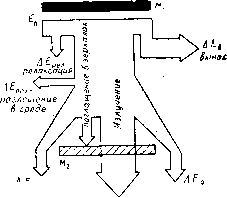

: f i

pac »acce»mje

дифракционньп r потери

Рис. 56. Баланс энергии в резонаторе

4.2. Расходимость лазерного излучения

4.2Л. Пространственные характеристики лазерного луча

Расходимость лазерного излучения на больших расстояниях от источника (в дальней зоне) определяется пространственной когерентностью выходного пучка, которая зависит от оптического качества активной среды лазера и характеристик резонатора.

Картина распределения интенсивности в дальней зоне (рис. 57, а) может быть получена с помощью скалярной теории дифракции, позволяющей рассчитать распределение интенсивности в любой точке на пути распространения лазерного излучения по известному распределению электромагнитного поля в выходном устройстве лазера.

В основе решения лежит математическое описание принципа Гюйгенса-Френеля: амплитуда волны в любой точке плоскости изображения является суперпозицией (суммой)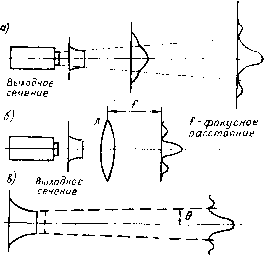

Дальняя зона

e = t.22 Л/Л

Выгодное сечение

Дальняя зона

Рис. 57. Расходимость лазерного излучения: а - формирование распределения интенсивности в дальней зоне, б - распределение интенсивности в фокальной плоскости линзы Л, s - влияние распределения интенсивности (-) и фазы (--) в выходном сечении лазерного пучка на распределение интенсивности лазерного излучения в дальней зоне

сферических волн, исходящих с поверхности источника электромагнитного излучения (рис. 58).

В плоскости с координатами ХоОоУо расположена область S, которая называется областью объекта или источника. В каждой ее точке считается известной амплитудно-фазовое распределение поля излучения и(Хо, уо)-ехр[/ф(Хо, уо)1 На некотором расстоянии расположена плоскость изображения, в которой введены координаты х,©,?/,. Требуется определить комплексную амплитуду в любой точке в плоскости изображения.

Рис. 58. Определение распределения, интенсивности в дальней зоне

Распределение интенсивности I{xi, yi) в дальней зонеоп- ределяется как квадрат модуля комплексной амплитуды:

НиУг) \u{x,y,)\UiXuУ) М*(С„У,)- (4-2);

Поле монохроматической волны U{Xi, yi) находится в со-] ответствии с принципом Гюйгенса-Френеля:

-cos(«,Zo,)rf5. (4.3)

Выражение (4.3) часто называют интегралом Кирхгофа.

Практический интерес представляет получение значений распределения интенсивности на больших расстояниях от плоскости объекта, в так называемой области дифракции Фраунгофера для

При выполнении этого условия можно ограничиться рассмотрением задачи только вблизи оси (параксиальное приближение), что существенно упрощает решение уравнений (4.2), (4.3). Интересно, что распределение интенсивности излучения монохроматического пучка в фокальной плоскости линзы (рис. 57, б) эквивалентно распределению интенсивности в дальней зоне. Это следствие того, что построение изображений с помощью сферических линз и зеркал является частным случаем более общего изложенного выше подхода. Результаты решения уравнений (4.2), (4.3) для некоторых наиболее характерных задач лазерной оптики приведены в табл. 4.1.

Под расходимостью лазерного излучения понимают угол 26, в пределах которого содержится определенная доля (см. табл. 4.1) мощности или энергии лазера. Для Гауссовых пучков в пределах угла расходимости интенсивность пучка падает в раз. Для остальных угол расходимости определяется направлением на первые дифракционные минимумы. Обозначая долю лазерного излучения, заключенного в угле расходимости, как у, можно оценить плотность энергии излучения д на расстоянии L:

£2 62

(4.4)

где Вл - энергия излучения на выходе из лазера. Размер фокального пятна при фокусировке лазерного излучения без учета аберраций:

7=6/, (4.5)

где / - фокусное расстояние оптической системы. При расфокусировке размеры пятна возрастают:

(4.6)

Где А / - степень расфокусировки.

Наименьший дифракционный угол расходимости при одинаковой выходной апертуре наблюдается для пучков с Гауссовым распределением интенсивности и только для них сохраняется профиль радиального распределения интенсивности по мере удаления от лазера.

Независимо от формы выходной апертуры важнейшее знание для угловой расходимости лазерного излучения имеют ее поперечные размеры (вернее, отношение %ld). Поэтому