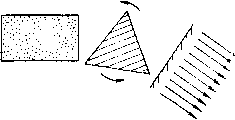Рис, 52. Схемы лазерных резонаторов со спектральными селекторами: а - дифракционной решеткой; б, в - плоскопараллельиым и клиновым интерферометром Фабри-Перо; г - дисперсионной призмой

4.1.2. Качество лазерного луча

Кроме" монохроматичности получаемое в резонаторе ла зерное излучение обладает такими показателями качества, как когерентность, поляризация, а также медовая структура

Когерентность -это согласованное протекание во време- ни нескольких колебательных или волновых процессов. При изучении лазерных пучков выделяют временную и пространственную когерентность. Временная когерентность связана со степенью монохроматичности световой волны и характе-» ризуется временем когерентности /ког=1/АУл, в течение ко-"

хирого возможный сдвиг фазы колебаний в пределах ширины линии излучения достигнет максимальной величины, или соответствующей этому времени длиной когерентности

Для газовых лазеров Ьког=« Ю... 10 м, а для твердотельных LKor~U,o мм. Это объясняется ббльшей шириной спектральных линии твердотельных лазеров, что связано с воздействием на излучающую частицу сильных элекгрических и магнитных полей кристаллической решетки, а также нали-iHtM неоднородностей в твердотельной матрице и, как пра-.1.10, небольшой длиной резонатора.

Для описания когерентных свойств волны в направлении, перпендикулярном направлению ее распространения, применяют термин пространственная когерентность, которая мо-,лсг характеризоваться объемом когерентности, т. е. обла-.1ью пространства, где волна сохраняет когерентность.

для количественной оценки когерентности излучения мож-,iO пользоваться коэффициентом контрастности интерференционной картины, образуемой в результате сложения двух лазерных пучков из одного источника, прошедших путь разной длины: V= Umax-/mm)/(/max+ -/111111), ГДе /щах И /щш-ИН-

lencHBHOcTb света в максимумах и минимумах интерференционной картины. Для когерентного излучения y--l, а в случае полной некогерентности vO-

Электромагнитное излучение, у которого направления электрического £ и магнитного Н полей сохраняются неизмененными в пространстве или изменяются по определенному закону, называется поляризованным. Направлением поляризации условились называть направление электрического поля Е(И±Е). Естественный свет неполяризован, его можно рассматривать как совокупность волн произвольной поляризации. Если в резонатор лазера не введены специальные поляризаторы, выделяющие световое излучение с определен-

ь1м направлением поляризации, то направление поляризации лазерного излучения произвольно. Часто в качестве се-ектирующего элемента в резонатор вводят прозрачную для "Злучения пластину, расположенную под углом Брюстера к "1:11 резонатора (в газовых лазерах эту роль могут играть ирцевые пластины разрядных трубок). Поскольку при прохождении излучения через такую пластину наименьшие по-ери будет иметь излучение, плоскость поляризации которого

Роходит через ось резонатора и перпендикулярна плоскости

пластины, то в резонаторе будет развиваться только излуче ние, имеющее соответствующую плоскость поляризации. Вы деление преимущественного направления поляризации осу ществляют также с помощью металлических зеркал, распо ложенных под углом к падающему излучению.

Резонатор Фабри-Перо, состоящий из двух плоскопараЛ! дельных зеркал, редко применяется в качестве лазерного ре- зонатора (например, в полупроводниковых и твердотельных лазерах в случае использования в качестве зеркал торцевых поверхностей кристаллов). Это связано прежде всего с большими потерями излучения в таких резонаторах. Поскольку размеры пучка всегда ограничены, то из-за дифракции на краях пучок расширяется в поперечном направлении и может выйти за пределы оптической системы. Угловое дифракционное расширение пучка с поперечным размером d составляет Qd = aWd), где коэффициент а зависит от формы поперечного сечения пучка. До обычных активных сред лазеров расстояние между зеркалами Ld, и потери из-за дифракции для инфракрасного излучения могут достигать 10 % и более. Поэтому резонаторы современных лазеров, как правило, состоят из плоских и сферических зеркал с разными радиусами кривизны отражающей поверхности г. Их свойства зависят от знака и величины радиуса кривизны и расстояния между зеркалами и определяются стабильностью существования в них электромагнитной волны. Критерием возможности использования для анализа распространения излучения волнового или геометрического приближения является число Френеля Nф: Nф=d/{}.L). ПриЛф»! для анализа распространения излучения можно пользоваться геометрическим приближением, а при Лф <1 необходимо учитывать волновые свойства света. Для лазерных резонаторов число Френеля может соответствовать как условиям волновой оптики (Лф~1), так я геометрическому приближению (Л/ф>1).

В геометрической оптике любое рассмотрение, как правило, начинают с луча света, распространяющегося в резонаторе на малом расстоянии от оптической оси под небольшим углом к ней (такой луч носит название параксиального)-

Схема резонатора со сферическими зеркалами Mi и Mi приведена на рис. 53. Расстояние между зеркалами L, а радиусы кривизны Г1 и Г2 положительны для вогнутых и отрицательны для выпуклых поверхностей. Если при многократных отражениях от зеркал расстояние луча от оптической

U i возрастает по мере роста числа отражений и он в конце ;,оицов выходит из резонатора, то в таком резонаторе потери б\дут велики. При этом относительная величина смещения положения луча на выпуклом зеркале за один проход называется коэффициентом увеличения резонатора М. В случае, когда луч остается вблизи оптической оси, резонатор характеризуется низкими потерями. Выполнив такой анализ для произвольного расстояния между зеркалами и произвольных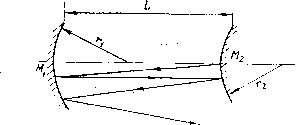

Рис. 53. Схема резонатора со сферическими зеркалами

радиусов кривизны, можно показать, что для резонатора с малыми потерями должно удовлетворяться условие устойчивости. Это условие обычно записывается в виде неравенства:

0<(1-L/r,) (1- -oXl-

Пока для резонатора выполняется это неравенство, параксиальные лучи остаются вблизи оптической оси даже после многих отражений, и такой резонатор называется устойчивым. В противном случае, если (1-L/ri) (1-L/rj) <0 или П-L/ri)(l-L/r2)>l, резонатор будет неустойчивым и после Многократных отражений луч удалится от оси. Величину коэффициента увеличения неустойчивого резонатора можно выразить через отношение радиусов зеркал M=ri/r2>l. Для Лазеров небольшой мощности наиболее распространенным является устойчивый резонатор с вогнутыми зеркалами или Эквивалентный ему резонатор с плоским и вогнутым зерка-ом. Подобные резонаторы легко юстируются, удобны в ра-те, излучение выводится через отверстие на оси выводного Ркала или через частично прозрачное покрытие на пропус-

кающей лазерный луч пЬдложке и имеет? в поперечном сече НИИ круглую форму.

Неустойчивые резонаторы, которые, как правило, приме няются для лазеров средней и большой мощности, также имеют определенные достоинства. Во-первых, даже в случае применения очень коротких резонаторов такого типа активная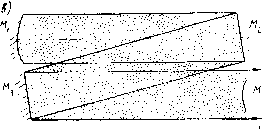

Рис. 54. Распростраиеиие излучения в резонаторах различных типов: а - устойчивом, б - неустойчивом, в - многопроходном

Среда в них используется очень эффективно. В типичном устойчивом резонаторе лазера пучок сжимается и становится очень узким (рис. 54, а). Вклад в усиление пучка дает только та часть активной среды, которая близка к оптической оси В неустойчивом лазерном резонаторе весь объем активной среды может участвовать в процессе усиления светз (рис. 54, б).

Второе достоинство неустойчивых резонаторов состоит удобстве регулировки и изменении размеров выходного све

тового пучка. Выходную мощность лазерного излучения можно изменять в широких пределах, варьируя расстояния между зеркалами. Прозрачность неустойчивого резонатора определяется не пропусканием одного зеркала, а геометрическими размерами системы и составляет: т=1 - Для вы-сокоэпергстических лазеров с большими объемами активной среды применяют многопроходные резонаторы (рис. 54, в),

°) ,г----------------- - п

Л/ / у у А/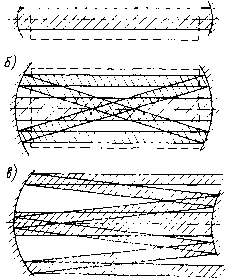

Рис. 55. Развитие поперечных мод в резонаторах: а - устойчивый , Лф п. 1; б - устойчивый, Лф > I, 8 - неустойчивый, Лф>1

позволяющие эффективно использовать в процессе генерации излучения всю активную среду.

Короткие резонаторы с большими поперечными размерами Нфкал (область больших чисел Френеля Мф;>1) вызывают \сложнение поперечной структуры лазерного пучка, что связано с развитием в резонаторе поперечных мод электромагнитных колебаний.

В лазерном резонаторе, характеризующемся небольшими плсламн Френеля Лф »1 (рис. 55, о), роль дифракции веника и все области усиливающей среды оказываются связан-