Интенсивность излучения, распространяющегося в определенном направлении (или плотность потока), h есть энергия, которая протекает через единичную площадку dS, перпендикулярную к направлению потока в единичном телесном угле с?ф, в единичном частотном интервале dv в единицу времени dt, IvdEy/idSdcpdvdt), где cf£v - количество лучистой энергии в частотном интервале (v, v + dv), проходящей через площадку dS внутри телесного угла d(p за время dt.

Интенсивность монохроматического излучения, проинтегрированная по частоте, дает интегральную интенсивность.

Поле излучения однородно, если / постоянна в любой точке; оно изотропно, если / не зависит от направления в любой точке. Некоторая область, через которую проходит электромагнитное излучение в любой момент времени, будет содержать определенное количество протекающей лучистой энергии. Эта электромагнитная энергия, содержащаяся в единице объема, определяет плотность электромагнитной энергии р: р= (£2 + Я2)/8я, где Е и Я -соответственно электрическое и магнитное поля.

Обозначая единичный объем dV я учитывая, что dSdt= = dV/c, можно записать выражение для энергии, присутствующей в dV в любой момент времени: dEv = Ivd(fdvdV/c. Излу-

чение со всех направлений, присутствующее в dV в любой момент времени, определяется интегрированием этого равенства по всем телесным углам и по всему объему V:

Разделив обе части равенства на V и dv, получим спектральную плотность энергии в единичном частотном интервале: pv=l/cj/vd9. Для изотропного излучения pv = 4n/v/c. Если излучение распространяется в виде узкого пучка с телесным углом Аф, плотность энергии излучения равна: pv= = 1Лц>/с.

В то же время ряд явлений, связанных с взаимодействием света с материей, главным образом со свечением и поглощением излучения, не могут найти достаточно строгого объяснения в рамках"волновой теории. Так, экспериментальная кривая спектральной плотности излучения термодинамически равновесных систем (спектр излучения абсолютно черного

Рис. I. Спектральная плотность излучения абсолютно черного тела, описываемая с помощью выражений, полученных В. Вином (/), Дж. Рэле-ем и Дж. Джинсом (2) и М. Плаиком (3)

тела) в области больших значений ЯГ>7,8-10 мкм К (Г -равновесная температура системы) хорошо описывается полученной на основе волновой теории формулой Рэлея- Джинса (см. рис. 1):

= 8irv»*r/c», (1.2)

где /г=1,38-10-23 Дж/К - постоянная Больцмана. При малых ЯГ<3000 мкм-К результаты экспериментов хорошо описываются формулой Вина !

8ic v2 /г-v Р„ =--

[кт)

где /1 = 6,63- 10-3* Дж-с -постоянная Планка.

В 1900 г. М. Планк, анализируя оба выражения - для области коротких и области длинных волн, нашел способ объединения этих формул в одно выражение, получить которое на основе известных в то время физических законов 6bUfio Чевозможно:

- . (1.3)

Планку удалось получить формулу (1.3), рассматривая излучение в полости в состоянии равновесия с ее стенками, т. е. для термодинамически равновесных систем, только введя принципиально новое предположение о том, что энергия, которую несет свет, может поглощаться и испускаться не непрерывно, а отдельными порциями. Эти элементарные, неделимые порции энергии он назвал квантами энергии e==hv. Рассмотрение предположения Планка совместно с энергетическим (точнее термодинамическим) анализом излучения привело Эйнштейна к заключению, что этот постулат есть следствие квантовых свойств самого излучения, что именно свет по своей природе несет элементарные порции энергии - кванты, что именно свет является квантованным, т. е. состоит из потока особых частиц (корпускул), названных позднее фотонами, каждая из которых несет порцию энергии, описываемую формулой Планка. При таком корпускулярном подходе ин-.тенсивность монохроматического света выражается через объемную концентрацию фотонов Пр и их энергию: /v = hvrip-c. На основании корпускулярной теории Эйнштейн просто объяснил и другое явление, не нашедшее объяснения с помощью волновой теории света, а именно - фотоэлектрический эффект, который состоит в том, что некоторые материалы, например, цинк, освещенные светом определенной частоты, испускают поток электронов. Это явление было подробно исследовано, однако попытки его осмысления с помощью волновой теории всегда приводили к противоречиям.

Еще одной проблемой, не решенной физиками на рубеже XIX-XX вв, был характер спектров элементов в газообразном состоянии, состоящих из отдельных спектральных линий, структура которых индивидуальна для каждого газа. Объяснить эту картину удалось лишь в 1911 -1913 годах Н. Бору на основе представлений квантовой механики. Согласно этим представлениям энергия электрона, связанного в атоме, а следовательно, и энергия атома в целом непроизвольна. Она может иметь лишь определенный дискретный ряд значений ео, Ki, ..., 8„, называемых уровнями энергии, или энергетическим спектром атома. Самый нижний уровень энергии ео (рис. 2), при котором энергия атома наименьшая, называется основным. Остальные уровни ei, Е2, ..., е™ соответствуют более высокой энергии атома и называются возбужденными. Сплошной спектр в верхней части рис. 2 начинается с энер-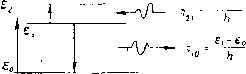

Рнс. 2. Энергетические уровни атома

ИИ боо И соответствует ионизированному состоянию атома, е. полному отрыву электрона от атома. При переходе атомного электрона с одного уровня на другой атом может излучать или поглощать кванты электро-. магнитного излучения, частоты которых определяются соотношением: Vmn= {ет-г„)/к. Разность энергий между уровнями внешних, валентных электронов атома соответствует, частотам или длинам волн (см. формулу (1.1)) видимого света; разность энергии между уровнями внутренних электронов больше, она соответствует рентгеновскому излучению.

Дискретность энергетического спектра свойственна не только атомам. Она присуща вообще любой системе взаимо-

действующих друг с другом микрочастиц: молекуле, иону твердому телу.

Молекула имеет гораздо большее число уровней энергии чем атом, что отражает сложность ее,строения. Одни из ни> также связаны с движением электронов. Разность энергий между этими уровнями, как и в атоме, велика, они соответ ствуют видимому и ультрафиолетовому свету и рентгеновс кому излучению. Другие уровни молекулы обусловлены ко лебаниями составляющих ее атомов около положения рав новесия. Разности энергий между этими уровнями меньше они соответствуют инфракрасному излучению. И, наконец есть уровни, связанные с вращением молекулы как целого Разность энергий между вращательными уровнями еще меньше, они соответствуют радиоволнам. В твердом теле электронный и колебательный спектры гораздо богаче, чем у изолированных атомов или молекул.

При переходе на более низкий уровень частица отдает энергию, а при переходе на более высокий - получает. Различают излучательные и безызлучательные квантовые пере-

е,. -

после. „ с/потиобения

"Рис. 3. Три типа квантовых переходов между уровнями; а - спонтанный; б - вынужденный, при котором поглощается фотон; в -вынужденный, при котором число фотонов увеличивается иа 1

ходы. При излучательных квантовых переходах частица излучает или поглощает электромагнитное излучение. В случае безызлучательных переходов частица получает или отдает энергию при взаимодействии с другими частицами (не фотонами) или системами частиц.

Рассмотрим, в первую очередь, взаимодействие частиц с электромагнитным излучением (рис. 3). 8

Если частица в данный момент времени находится в одном из возбужденных состояний Вт, то такое состояние неустойчиво, даже если на него не влияют другие частицы. Через некоторое время частица перейдет в одно из состояний с меньшей энергией en. При этом она излучит квант света с частотой Vmn и энергия электромагнитного поля увеличится на величину hvmn (рис. 3, а). Такой самопроизвольный (спонтанный) переход с одного уровня на другой и сопровождающее его спонтанное излучение столь же случайны во времени, как радиоактивный распад атома. Основная характеристика спонтанных переходов - среднее время At, через которое происходит переход, или обратная ему величина Атп, называемая коэффициентом Эйнштейна для спонтанного перехода и имеющая смысл вероятности.

Случайность спонтанных переходов приводит к тому, что различные атомы излучают неодновременно и независимо. Излучение всех обычных источников света (ламп накаливания, газоразрядных ламп и др.) возникает за счет актов спонтанного испускания.

Если частица находится на нижнем уровне вп, а электромагнитное излучение, падающее на вещество, содержит кванты света частотой Vmn, то может произойти переход частицы на уровень е™, при котором атом поглощает квант излучения (рис. 3, б). Такие вынужденные переходы называются резонансными и характеризуют поглощение света.

Анализируя процессы, связанные с поглощением и испусканием квантов света веществом, находящимся в термодинамически равновесном состоянии, А. Эйнштейн в 1916 г. пришел к выводу, что для поддержания равновесия в системе должен существовать еще один механизм взаимодействия света с веществом - так называемое стимулированное (или индуцированное) излучение. Частица, находящаяся в возбужденном состоянии, может перейти с уровня е,п на уровень e„ не спонтанно, а под действием кванта света, если только его частота достаточно близка к частоте перехода Vmn=(em- -en) i. Такие переходы также называются вынужденными (рис. 3, в).

Особенность стимулированного излучения заключается в том, что «новорожденный» квант света абсолютно не отличим от вызвавших переход «первичных» квантов: он имеет те же частоту и фазу, направление движения и поляризацию.