Дрейф электронов и дырок (как разноименных зарядов) под действием электрического поля происходит в противоположных направлениях, поэтому суммарная плотность дрейфового тока в кристалле

Лр = in ЯР + /ряр = {шп + Au.p). (2.25)

Коэффициент пропорциональности между напряженностью поля £ и плотностью тока /щ, составляет удельную проводимость

c = l/p=e(ftM.„-f piip), (2.26)

где р - удельное сопротивление.

В собственном полупроводнике Пг=ри поэтому удельная проводимость полупроводника

°/="/(.«+)- (2-27)

В примесном п-полупроводнике ПпРп и Хп>Хр, а в р-полупроводнике рр:>Пр и Хр>,1и, поэтому удельная проводимость соответственно

с„-«е/г„,и.„ и ffpRe/Jp,u.p. (2.28)

Собственная электропроводимость обусловлена генерацией электронно-дырочных, пар, а примесная - ионизацией атомов примеси.

Температурная зависимость удельной проводимости определяется главным образом температурной зависимостью концентрации носителей зарядов. Экспоненциальное увеличение концентрации щ {см. формулу (2.16)] с повышением температуры у собственных полупроводников предопределяет такой же характер температурного увеличения собственной проводимости а, (рис. 2.8, а).

В примесном полупроводнике в низкотемпературной области (7i<-60° С) степень ионизации примеси мала, поэтому невелика и проводимость Gn и Ор. При повышении температуры возрастают ионизация примеси и проводимость. В рабочем диапазоне температур (от Ti=-60° С до 72=+ 100° С) при полной ионизации примесей концентрация основных носителей пир практически постоянна, поэтому проводимость Gn и Ор почти не меняется. Некоторое снижение проводимости в рабочей области происходит за счет умень-тнения подвижности носителей заряда. При температуре Т свыше критической {Т>Т2) наступает интенсивная тепловая генерация, что вызывает рост концентрации носителей и проводимости и пре-врашение полупроводника в полуметалл.

Диффузионное движение частиц возникает между двумя элементарными объемами Vi и Уг полупроводника (рис. 2.8, б) с различной концентрацией носителей {Ni>N2). Предположим, в объеме Vi имеются подвижные электроны, а в объеме V2 - дырки. В каждом объеме заряды подвижных частиц скомпенсированы противоположными по знаку зарядами неподвижных частиц. Каждый объем электронейтрален. За счет разности концентраций частиц между объемами возникает диффузия электронов из объема Vi в объем V2 и дырок в обратном направлении.

Диффузионное движение частиц будет сопровождаться перераспределением электрических зарядов, что приведет к возникновению в структуре полупроводника внутреннего электрического поля. Под действием сил внутреннего поля возникнет дрейфовое движение частиц в направлении, противоположном их диффузионному перемещению. В условиях равновесия должны быть равны плотности дрейфового и диффузионного токов.

В случае одномерного движения плотность электронного и дырочного диффузионного токов пропорциональна величине заряда е одиночных носителей (с учетом их знака), коэффициенту их диффузии Dn и Dp, градиенту концентрации электронов da/dx и дырок dp/dx (взятому с обратным знаком, так как движение происходит в направлении, противоположном градиенту концентрации);

Jnm = eDn{dnjdx); Урд„ф= - eDp{dp]dx).

Коэффициенты диффузии электронов £>„ и дырок Dp определяются числом носителей заряда, которые диффундируют за 1 с через элементарную площадку (см/с). Коэффициенты диффузии связаны с подвижностью соотношением Эйнштейна

D„ = \>.nkTie к Dp= pkTJe. (2.29)

Коэффициенты диффузии однозначно определяются подвижностью носителей, поэтому, как и подвижность, они в большей степени зависят от концентрации и в меньшей от температуры.

Плотность суммарного диффузионного тока в полупроводнике с неоднородной концентрацией свободных электронов и дырок

/яиф = /плиф -Ь Уряиф = е {Dndjdx - Dpdpjdx). (2.30)

Плотность полного тока. В объеме полупроводника плотность полного тока, обусловленная дрейфовым и диффузионным перемещениями свободных носителей заряда, в соответствии с формулами (2.25) и (2.30):

/ = Лр -Ь /диФ = е£ (и!1„ + piip) + -f- eDn{dnldx) - eDp{dpldx). (2.31)

Все слагаемые этого уравнения содержат значения концентрации электронов и дырок, которые при одномерном движении являются функциями координаты расстояния х и времени t.

Уравнения непрерывности. В любом объеме полупроводника наряду с диффузионным и дрейфовым движениями свободных электронов и дырок протекают процессы генерации и рекомбинации. В отдельных частях кристалла эти процессы могут иметь разную-интенсивность, однако во всем объеме должен соблюдаться закон сохранения количества электричества. Это значит - изменение-плотности объемного заряда в объеме в единицу времени должно равняться числу приходящих или вытекающих из этого объема элементарных электрических зарядов.

. Связь между изменением концентрации носителей в элементарном объеме полупроводника и током, проходящим через этот объем, устанавливается уравнениями непрерывности:

dp dt dn dt

Ро

n - По

ряиф

+ Д«яиф

(2.32)

В правых частях уравнений: первое слагаемое {gn и gp) характеризует скорость генерации, обусловленную внещними причинами; второе слагаемое - скорость изменения избыточной концентрации,, т. е. время рекомбинации неравновесной концентрации частиц; третье слагаемое - диффузионное движение, а четвертое и пятое - их дрейфовое движение.

Уравнениями пользуются при анализе процессов в полупроводниковых приборах. Например, если генерация отсутствует {gp = -gn=0), а действием электрического поля можно пренебречь {dE/dx=0), уравнения непрерывности упрощаются и приводятся к уравнениям диффузии вида

J- Dpd2p/dx2-{р- Po)hp = 0; Dnd2nldx2 (« По)/-с„ = 0. (2.33)

Решения этих уравнений позволяют установить закон измене-ния концентрации неосновных носителей вдоль координаты х. Ес-ли длина кристалла полупроводника w велика и превышает среднюю диффузионную длину носителей w>Lp,

(2.34>

Ар = V Р>рр,

ТО изменение концентрации частиц, например типа р, происходит ПО экспоненциальному закону (рис. 2.9, а), где ро - равновесная /концентрация дырок.

Средняя диффузионная скорость, с которой носители проходят диффузионную длину,

(2.35)

Если длина кристалла невелика {w-Lp), решения уравнения показывают, что закон распределения носителей линеен (рис. 2.9, б). Средняя диффузионная скорость для этого случая идиф будет а) иной, а среднее время диффузии дырок

- д = ™/<„Ф = ™2/20р. (2.36)

Аналогичные выражения можно получить, . используя электроны в качестве основных носителей заряда в структуре полупроводника.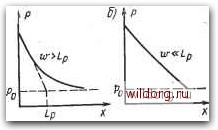

Рис. 2.9. Графики изменения концентрации частиц при диффузии