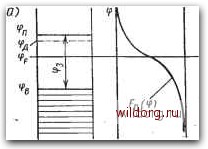Рис. 2.7. Положение уровня Ферми и функция распределения электронов в при-, . месном полупроводнике

п-полупроводнике уровень Ферми смещается в зону проводимости, а в р-полупроводнике - в валентную зону.

В примесном электронном полупроводнике при комнатной температуре {Г=300 К) концентрация донорных атомов значительно превышает собственную равновесную концентрацию электронов Прщ. В рабочем диапазоне температур донорные атомы практически полностью ионизированы, поэтому концентрация свободных электронов п определяется концентрацией примеси, т. е. п=Мд, и не зависит от температуры. Вследствие этого уровень Ферми в примесном электронном полупроводнике согласно выражению (2.18)

ff --=Е+ HJh) = + fc (д/п) (2.19)

лежит тем выше (см. рис. 2.7, а), чем больше концентрация доноров Лд и чем ниже температура, от которой экспоненциально зависит собственная равновесная концентрация nt и максимальная концентрация электронов Л/п в зоне проводимости.

Значение уровня Ферми действительно в узком диапазоне температур Tl-Гг. Нижняя граница диапазона Ti ограничивается температурой ионизации примесей, а верхняя Гг - критической температурой полупроводника, при которой электронный полупроводник превращается в собственный из-за роста концентрации носителей Hi (табл. 2.2).

Из табл. 2.2 следует, что кремний при одинаковой с германием концентрации донорной примеси Л/д имеет более высокий потенциал ионизации фпд (энергетический интервал между донррным уровнем и зоной проводимости), вследствие чего обладает более высокой термостабильностью.

Т а б л и ц а 2.2

Для ярко выраженного дырочного полупроводника р-типа .{р п), в котором акцепторы полностью ионизированы и температура ниже критической, справедливы аналогичные соотношения:

P(F = fE-fM-Fi) = \-(MJ.) (2.20)

а уровень Ферми лежит тем ниже, чем больше концентрация акцепторов и чем меньше температура (см. рис. 2.7, б).

Скомпенсированный полупроводник можно получить, если вето структуру ввести равные концентрации донорной и акцепторной примесей {Na=Njx). Он обладает свойствами основного полупроводника и отличается от него лишь временем жизни носителей заряда и их подвижностью.

§ 2.6. Процессы электропроводности полупроводников

Движение носителей заряда. Различают тепловое, дрейфовое и диффузионное перемешения элементарных частиц в структуре полупроводника.

Тепловое движение свободных носителей заряда совершается в кристалле полупроводника хаотически. Поскольку все направления этого движения равновероятны, ток в кристалле равен нулю. Тепловое движение свободных частиц характеризуют среднестатичес-кими длиной /ср и временем tcp свободного пробега (между столкновениями с другими частицами или узлами кристаллической решетки) и тепловой скоростью

i;,. = Y SkT/m*, (2.21)

зависящей от температуры Т. В результате взаимодействия частиц изменяются их скорость и направление движения, происходит их рассеяние. Центрами рассеяния служат неоднородности кристаллической решетки. Они создаются атомами примесей, а также дефектами решетки. На различных центрах рассеяния процессы имеют различную физическую природу, поэтому длина свободного пробега частиц колеблется /ср= 10---10-2 см. При Г=:300 К средняя тепловая скорость г;т~10 см/с.

Дрейфовое движение электронов и дырок совершается в структуре полупроводника под действием электрического поля и является направленным. Направленное дрейфовое движение носителей заряда встречает ряд специфических для твердых тел препятствий. Они создаются дефектами структуры и тепловыми колебаниями атомов решетки и примесей.

Направленное движение (дрейф) носителей в электрическом

тюле характеризуют дрейфовой скоростью

t; = (e£/m*)ep. (2-22)

где еЕ/т* ~ ускорение электрона в поле с напряженностью Е; т* - эффективная масса частицы в кристалле.

При малой напряженности поля 10 В/см &др~ 10*Ч-10 см/с и

»др<Ут.

Подвижность носителей заряда р 1см2/(В-с)] характеризует их направленное движение и определяется их средней- дрейфовой скоростью в электрическом поле с напряженностью £=1 В/см:

«яр еВ

[ е \

(2.23)

Подвижность обратно пропорциональна эффективной массе частиц. Эффективная масса электронов меньше эффективной масськ. дырок (тп*<тр*), поэтому их подвижность больше (,in>fAp)-Для германия pn/.ip = 3800/1800~2,l и для кремния ,in/,ip= 1400/500 =«2,8.

На подвижность носителей заряда в основном влияют два физических фактора: тепловые колебания атомов кристаллической решетки (рассеяние носителей заряда на тепловых колебаниях атомов кристаллической решетки) и электрические поля ионизированных примесей (рассеяние на ионах примесей).

В нижней области рабочего диапазона температур рассеяние вызывается дефектами решетки и атомами примеси. При низкой температуре уменьшаются тепловые скорости движения носителей заряда, увеличивается длительность воздействия электрического поля примеси на носитель заряда и подвижность уменьшается при уменьшении температуры.

В диапазоне больших температур преобладает рассеяние носителей заряда на ионах примеси и тепловых колебаниях атомов-кристаллической решетки, поэтому с увеличением температуры в этой области подвижность носителей снижается. Рост концентрации носителей сопровождается более частым столкновением частиц,, уменьшением длины их свободного пробега и подвижности.

Электропроводность полупроводников. Направленное движение электронов и дырок в полупроводнике под-действием электрического поля создает в нем дрейфовый ток. Плотность электронного in др и дырочного /р др токов:

/пдр = env = enEin< JpB.p = epvjip = epEiip, (2.24>

где пир - концентрации электронов и дырок; [х„ и [Хр - подвижности электронов и дырок.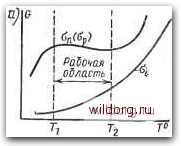

Рис. 2.8. К объяснению явления диффузии