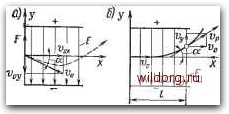Рис. 10.6. Траектории электрона в однородном электрическом поле

зарядом, создаваемым самими частицами) являются: движение частиц в однородном электрическом или в однородном магнитном полях, а также их движение в скрещенных электрическом и магнитном полях. При рассмотрении характера движения частиц ограничимся изучением траекторий электронов, так как другие носители заряда, например положительные ионы, имеют аналогичные в геометрическом отношении траектории.

Траектории электронов в однородном поле. Предположим, между параллельными плоскостями (рис. 10.6, а) действует однородное электрическое поле. Однородное поле обладает одинаковой напряженностью в любой точке как по величине, так и по направлению. Допустим, в это поле с напряженностью Е влетает электрон с начальной скоростью оо, направленной под некоторым углом а к направлению поля. Начальную скорость электрона можно разложить на две составляющие Vox и Voy, направленные соответственно по оси X VI у прямоугольной системы координат. На электрон в электрическом поле будет действовать постоянная по величине сила F, направленная по оси у, равная произведению заряда электрона е на напряженность Е поля.

F = -еЕ.

(10.4)

В соответствии со вторым законом Ньютона постоянно действующая сила вызывает равноускоренное движение с ускорением, прямо пропорциональным величине силы F и обратно пропорциональным массе частицы т, к которой приложена эта сила.

ay = Flm = {elm)E.

(10.5)

Очевидно, если направление силы поля jF совпадает с направлением начальной составляющей скорости toy, электрон движется вдоль оси у равноускоренно и проходит путь:

(10.6)

В направлении оси х потенциал поля не меняется, поэтому в этом направлении на электрон никакие силы не действуют. В этом направлении он движется равномерно с начальной составляющей скорости Wo ж и проходит путь:

x = voJ. (10.7)

В результате электрон одновременно совершает равномерное движение в направлении оси х и равноускоренное в направлении оси. Уравнение траектории результирующего движения электро-

на получим, подставляя в уравнение (10.6) значение времени =д;/иол: из выражения (10.7):

0(/ . еЕ.

у =-л + т;--х"- (10.8)

Полученное выражение представляет собой уравнение параболы вида y=px + qx, следовательно, электрон, влетающий в однородное электрическое поле с начальной скоростью Vq, движется в этом поле по параболической траектории (см. рис. 10.6,а). За пределами поля электрон будет двигаться по прямолинейной траектории касательной к параболе в точке, где прекратилось действие поля на электрон.

Если электрон влетает в электрическое поле с начальной скоростью 0, перпендикулярной направлению силовых линий поля (рис. 10.6,6), то Voy = 0, а Vox = vo. В этом случае уравнение движения (10.8) электрона примет вид

y=[eE/(2mvl)]x2. (10.9)

Траектория движения электрона также будет параболой. Двигаясь по параболической траектории, он изменяет направление движения и скорость.

Если электрон влетает в однородное поле с начальной скоростью Vo, направленной вдоль силовых линий поля, то Voy = vo, а Vox = 0, тогда уравнения движения (10.6) и (10.7) электрона примут вид

y = Voyt+(eE/2m)t2; х = 0. (10.10)

Из первого уравнения следует, что электрон движется по прямолинейной траектории (вдоль оси у). При этом, если начальная скорость электрона совпадает по направлению с направлением действующей на электрон силы F (см. рис. 10.6, а, направление силы F противоположно направлению напряженности поля Е), то он движется в ускоряющем поле равноускоренно. Если же направление начальной скорости будет противоположно направлению силы, то электрон движется в тормозящем поле равнозамедленно. Это движение описывается уравнениями равнозамедленного движения:

у = {eE12m)fi-vt; v = v - {eE}tti)t. (10.11)

Пройдя некоторое расстояние, электрон может, израсходовав начальную энергию, остановиться, а затем под действием сил поля двигаться в обратную сторону уже равноускоренно.

Ускорение электронов электрическим полем. При ускоренном движении электрон приобретает наибольшую скорость и кинетическую энергию в конце своего пути. Кинетическая энергия W, приобретенная в электрическом поле,

Wm{v2-vl2, (10.12)

где г)о и - скорости электрона в начальной и конечной точках пути.

Работа сил поля по перемещению электрона из некоторой точки Л в точку Б равна произведению заряда электрона на разность потенциалов этих точек

we = {-e)(UA-Ui). (10.13)

Учитывая, что ибиа, разность потекциалов Ua--U, тогда

we = {-e){-U) = eU.

Согласно закону сохранения энергии увеличение (или уменьшение) кинетической энергии движущейся частицы равно работе, которая затрачивается на движение частицы,

Wk = We или m{v2 - vl)/2 = eU-. (10.14)

Если электрон вначале находится в состоянии покоя (t»o=0), то из уравнения (10.14) его конечная скорость

V = /2(е/ш)СЛ = Y2(\,6-10-19/9,1 • lO-ai) U =

= 5,93.105/f7 м/сагбОО/СА км/с. (10.15)

Эти соотношения справедливы лишь до тех пор, пока масса может рассматриваться как постоянная величина (m==mo), т. е. пока скорость электрона v мала по сравнению со скоростью света с (и<0,1 с). При этих условиях пройденная электроном разность потенциалов определяет энергию и одновременно скорость электрона. Из выражения (10.15) следует, что скорость движения электрона в электрическом поле зависит только от разности потенциалов и в начальной и конечной точках пути и не зависит от формы пути. Поэтому скорость электронов условно можно выразить в вольтах. Например, если условная скорость электрона равна 1 В, то из выражения (10.15) его действительная скорость f = 600V"l = =600 км/с.

Из выражения (10.14) можно получить единицу энергии, называемую электрон-вольтом, часто используемую в электронике. Энергия в 1 электрон-вольт (эВ), равная количеству энергии, которую приобретает электрон, пройдя разность потенциалов в 1 В, составляет

1 эВ= Ы,6-10-19= 1,6-10-19 Дж.

Скорость электрона в вольтах численно равна его кинетической энергии в электрон-вольтах.

Время пролета одиночным электроном расстояния L между двумя электродами, к которым приложена разность потенциалов U, определяется его средней скоростью движения

v={vo + v)/2. . (10.16)