поле конденсатора. В моменты ti, ts напряжение на конденсаторе равно нулю, ток максимален, а энергия сосредоточена в магнитном поле катушки. В процессе этих изменений (колебаний) на пластинах конденсатора возникает переменное напряжение, а в контуре протекает переменный ток; энергия электрического поля периодически превращается в энергию магнитного поля. После отключения контура от источника в нем возникают свободные колебания (колебания без внешнего источника энергии). Амплитуда колебаний определяется количеством первоначально полученной энергии, а период и частота - параметрами контура.

В процессе свободных колебаний в контуре без потерь напряжения на катушке и конденсаторе одинаковы, через них протекает один и тот же ток, а реактивные сопротивления конденсатора и катушки равны между собой: Xl=Xc или 2nfoL=lj{2nfoC), отсюда частота и период свободных колебаний:

/о = 1/(2л /ГС); г = 1 о = 2яУ/:с. (22.1)

Пример. Индуктивность катушки контура 10 мкГн, емкость конденсатора С=15 пФ. Определить fo и 7 в контуре:

/о = 1/(2л; .С) = 1/(2л;/10-10-б.15.10-12)я13.10б Гц; Г = 1 о= 1/13-10б«7.6-10-8с.

Затухание колебаний в контуре. Реальный контур обладает активным сопротивлением, на котором часть энергии превращается в тепло, поэтому свободные колебания постепенно убывают (затухают) по амплитуде (рис. 22.2, а). Для снижения тепловых потерь энергии подбором элементов L и С стремятся уменьшить активное сопротивление контуров. Однако затухание амплитуд свободных колебаний тока и напряжения зависит не только от значения активного сопротивления, но и от соотношения величин L и С, поэтому свойства контуров оценивают добротностью.

Под добротностью понимают отношение индуктивного или емкостного сопротивления контура на частоте fo свободных колебаний к его активному сопротивлению

2nfoL L

(22.2)

-r/LC

Хороший контур имеет добротность порядка сотен. В таком контуре амплитуда свободных колебаний затухает медленно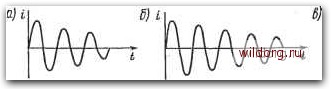

Рис. 22.2. Затухающие свободные колебания

(рис. 22.2, б). Величина, обратная добротности, называется затуханием контура

d=\iQ = rl\TiC.

Скорость снижения запаса колебательной энергии в контуре характеризует декремент затухания. Он показывает, какую часть своей энергии теряет контур за половину периода, и составляет

V n,d= n/Q =- л,г/->/Uc". (22.3)

Контуры с большим значением активного сопротивления относят к апериодическим. В них энергия, полученная в течение первого полупериода колебаний, превращается в тепло, и колебательный процесс на этом заканчивается (рис. 22.2, в).

Исследования показывают, что колебания в контуре возможны лишь при условии r<:2V L/C. Величина V L/C является важной характеристикой контура и называется волновым сопротивлением

Р = yZTc: (22.4)

Волновое сопротивление равно реактивному сопротивлению контура на частоте свободных колебаний:

= 2л/о/. = 2яА 11 /(2л KiC) ] - /Z./C = р; = 1/(2я/оС) = 2я YLC/(2nC) = VtjC = р.

(22.5)

Декремент затухания с. учетом выражения (22.4) можно представить

(22.6) (22.7)

Из выражений (22.2) и (22.3) следует, что

Q = Р/г.

пример. /.= 10 мкГн; С=1Б пФ; г=3 Ом. Определить р и Q: Р = VlJC = /10.10-6/15.10-12 = 815 Ом; Q=p - = 815/3 « 270.

Вынужденные колебания в последовательном контуре. Для получения незатухающих колебаний в контуре необходимо компенсировать потери энергии на его активном сопротивлении. С этой целью контур (рис. 22.3, а) подключают к внешнему источнику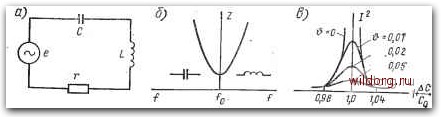

Рис. 22.3. Последовательный колебательный контур и его характернстнкн

переменной э. д. с. е=Ет8тЫ. Под действием этой э. д. с. в контуре возникают вынужденные незатухающие колебания. Действующее значение напряжения на зажимах внешнего источника

и = fz =гу г2+(хх)2, [(22.8)

где / - действующее значение тока в контуре;

Z - модуль полного сопротивления контура;

г - активное сопротивление контура; хь - индуктивное сопротивление катушки индуктивности; Хс - емкостное сопротивление конденсатора.

Когда реактивные сопротивления оказываются равными между собой {xl=Xc), в контуре наступает резонанс. Частота внешнего генератора /=1/(2п УЬС) совпадает с частотой собственных колебаний контура fo. Такой режим может быть достигнут изменением параметров контура или частоты генератора, питающего контур. При резонансе (когда Xl=Xc) полное сопротивление контура равно его активному сопротивлению (z=r), а поскольку г мало, ток в контуре максимален:

Ip=l7/r==nl7/vp, (22.9)

где г = gv/n.

При резонансе (xl=Xc) на катушке и конденсаторе создаются равные по значению, но противофазные напряжения Ul=Uc, где Ul=IpXl и Uc=IpXc. Эти напряжения компенсируют друг друга, поэтому согласно (22.8) напряжение внешнего источника U= z=Ur=Ipr. Соотношения напряжений на реактивных элементах и внешних зажимах источника

иии = UclU = Ixjir = xjr.

Учитывая, что на резонансной частоте согласно (22.4) Хь=р, поэтому

UJU = р/г = Q или f/i = С/с = QU. (22.10)

Отсюда следует, что напряжения на реактивных элементах контура при резонансе в Q раз превышают напряжение внешнего источника, поэтому резонанс в последовательном контуре получил наименование резонанса напряжения.

Сопротивление последовательного контура

2 = /г2 + (д: - х)2 = /г2 + [2nfL-1 /(2я/С)]2

зависит от частоты f питающего напряжения генератора. Если эта частота ниже частоты собственных колебаний контура (f-<fo), то емкостное сопротивление преобладает над индуктивным и контур для источника сигнала имеет сопротивление емкостного характера. Если частота питающего напряжения больше собственной частоты контура (f>fo), то индуктивное сопротивление больше емкостного и контур для источника сигнала имеет сопротивление индуктивного характера. При резонансе {f-fo) сопротивление пос-