меньше, и это дает равнодействующую в направлении, соответствующем наблюдаемому.

На основании данного объяснения очень трудно получить количественный результат, так как у нас нет какого-либо определенного способа для того, чтобы связать вращение с циркуляцией-даже в случае цилиндра). Прандтль предпринял героическую попытку определить хотя бы максимум подъемной силы L, который, как он утверждал, достигается тогда, когда значение циркуляции определяется при условии, что имеется одна-единственная критическая точка ).

Основываясь на этом, он нашел, что максимум коэффициента Cl равен 4ic. Недавно это значение было превышено) - еще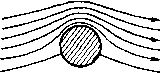

Рис. 3. Эффект Магнуса.

один факт, показывающий ненадежность нестрогих рассуждений.

Несостоятельность существующих объяснений эффекта Магнуса еще более ярко показывает следующий парадокс эффекта Магнуса.

Парадокс эффекта Магнуса. При малых скоростях вращения направление отклонения в действительности противоположно тому, которое дает объяснение Рэлвя (и которое наблюдалось Магнусом) *).

Для того чтобы объяснить этот парадокс эффекта Магнуса, нужно, по-видимому, учесть турбулентность пограничного слоя-

) Как показано в § 8, в случае сферы мы при.ходим даже к более глубокому парадоксу: вследствие односвязности циркуляция Г = 0.

Доводы Прандтля изложены в ([3], § 27); для цилиндра радиуса с при относительной поступательной скорости а циркуляция Г = 4 пса. По поводу более поздних экспериментальных данных см. [50], § 239.

Swanson W. М.. Final Report on Contract DA-33-019-ORD-1434, Case Inst. Technology, December 31, 1956. При У = ис=17а коэффициент Cl = 14,7 и «продолжал возрастать с постоянной скоростью>. Недавно, Glauert М. В. (Ргос. Roy. Soc. А242 (1957), 108-115) подверг вывод Прандтля критике, исходя из теоретических соображений.

*) См. [3], § 27 и 221; экспериментальные данные (в случае сферы) получил Маккол. Данные, приведенные в [3], § 239, показывают, что, по-внди-мому, аналогичная ситуация имеет место и для цилиндра.

jf 9. Эффект Магнуса; деривация 33

явление, которое до сих пор пе поддается математическому исследованию как краевая задача. Таким образом, при любом корректном истолковании реальной поперечной силы при малых скоростях вращения надлежит учитывать число Рейнольдса)

Явление «деривации» аналогично эффекту Магнуса. Артиллеристам уже более ста лет известно, что вращающиеся снаряды имеют тенденцию отклоняться от вертикальной плоскости, в которой производится стрельба, и что такое отклонение происходит в направлении вращения головки снаряда. Однако это явление в течение многих лет понималось неправильно ).

Одно неверное объяснение было предложено известным математиком - Пуассоном. Он считал, что вследствие инерции ось снаряда отстает от направления касательной к траектории.

.е/ (наряд

Меньшее давлен

Направление. Оерипации

Больи/сс Оавлаиип б

Рнс. 4. Объяснение эффекта Магнуса, по Пуассону.

как схематически показано на рис. 4, а. Следовательно, на нижней стороне должно создаться большее давление, а значит и большее трение. В соответствии с рис. 4, б это должно привести к отклонению в наблюдаемом направлении. Ошибочность объяснения Пуассона становится очевидной, если применить его к вращению теннисного мяча: получилось бы направление отклонения, противоположное обычному эффекту Магнуса!

Правильное объяснение заключается в следующем. С помощью количественного исследования гироскопической устойчивости можно установить, что устойчивое положение оси снаряда (с правой винтовой нарезкой) находится справа от касательной к траектории, а не выше ее, как это утверждал Пуассон. Таким образом, деривация снаряда вызывается главным образом не-

) См. Кг а lin е., Аег. Set.. 23 (1956, 377-378. *) Интересный исторический обзор дан в [5], гл. X.

посредственно аэродинамической поперечной силой и лишь косвенно - вращением.

Это опять-таки показывает ненадежность качественных соображений. Вероятность того, что случайное объяснение окажется правильным, равна 50%!

§ 10. Волновое лобовое сопротивление тонких крыльев

Парадокс Даламбера нельзя распространить на сверхзвуковое течение: даже без учета вязкости математические соображения приводят к существованию положительного лобового сопротивления. Ввиду парадокса обратимости это возможно только потому, что краевая задача (для стационарного движения), определяемая уравнениями Эйлера, не является корректной. Мы покажем сейчас это, начав с рассмотрения линеаризованного сверхзвукового течения (теория «тонкого крыла»).

Рассмотрим семейство независимых от времени сжимаемых течений, зависящих от параметра 8 - толщины крыла. Мы предполагаем (гипотеза (Е) из § 1), что потенциал скорости можно записать в виде

U = ax-\-bfix, у. г)-+0(82). (14)

Подставляя его в формулу(10) и делая обычные в теории возмущений допущения, мы получаем •) при 8-vO

{М2-1)?,, = ?уу + ?„. Ма/с. (14*)

Ясно, что случаям дозвукового течения (М<1), звукового течения (М = 1) и сверхзвукового течения (М > 1) отвечают уравнения в частных производных соответственно эллиптического, параболического и гиперболического типов*). Это простое замечание уже указывает на то, что краевая задача корректно поставлена лишь в дозвуковом случае.

В случае плоского течения 9 = <р(х, у) еще со времен Даламбера известно, что общее решение уравнения (14*) имеет вид

ф = Г(х~УМу)-ЬО{х-ьУШу), (15)

где F{r) и G(s) - произвольные функции.

) См. [6], § 141 или [101, стр. 245. Более подробное описание приложений см. в [10], гл. VIII.

) Это верно также и без линеаризации, но в таком случае М будет зависеть от координат. Следовательно, возможны трансзвуковые потоки и соответствующие им дифференциальные уравнения смещанного типа (эллиптические в одних областях и гиперболические в других), как показано в § 6. [Смешанным течениям посвящена обширная литература; см., например, [7*1 и [8»].-Ярил, ред.]