влечет обращение величин D и L (хотя и не М) ), а не оставляет их неизменными.

Поучительно проанализировать предыдущее противоречие подробнее. Пока не установлено, что краевая задача в § 5 корректно поставлена, нельзя делать вывод о том, что ее уравнения ошибочны. Возможно, что потребуется ввести какое-нибудь дополнительное условие. Действительно, как мы увидим в § 10, это может оказаться справедливым для сверхзвукового течения (т. е. если число Маха М> 1). Чтобы пояснить это, проведем следующее разграничение:

Определение 2. Будем называть гидродинамические теории неполными, если соответствующие условия определяют обтекание данного препятствия не единственным образом; переопределенными, если эти условия математически не совместны; ложными, если корректно поставленная задача дает грубо ошибочные результаты.

Теорема 1. Всякая обратимая гидродинамическая теория в отношении расчета лобового сопротивления и подъемной силы является неполной, переопределенной или ложной.

Дозвуковой случай. В дозвуковом случае, М < 1, по крайней мере для достаточно малого числа Маха недавно было показано 2), что краевая задача, определяемая уравнениями (И), (9) и (7*) из § 5, является корректно поставленной. Поскольку эта задача эллиптического типа, ее математическое решение U{x) должно быть аналитическим. Отсюда мы заключаем, что уравнения Эйлера - Лагранжа дают ложную теорию для стационарного дозвукового потока.

Околозвуковой случай. По поводу этого случая, когда в дозвуковом потоке имеются локальные сверхзвуковые зоны, высказано много различных и противоречивых утверждений. Были построены математические модели подобных околозвуковых течений ), но они, по-видимому, очень слабо отражают физическую

) Классическая гидродинамика правильно предсказывает тенденцию осе-симметрнчных препятствий подставлять потоку более широкую сторону: ср. [7], § 71, 124. {В случае тел, обладающих продольной симметрией, при обращении потока L остается неизменным, а у Л1 изменяется знак.)

2) Graffi D., Л Rat. Mech. Analysis, 2 (1953), 99-106; Gilbarg D., там же, 233-251; Gilbarg D. and Serrin J., там же. 4 (1955), Ш9-175; Bers L., Comm. Pure Appl. Math., 7 (1954), 441-504; Finn R. S. and Gilbarg D., там же, 10 (1957), 23-64 и Acta Math.. 98 (1957), 265-276. Это обобщает результат из § 4 на случай М = О (задача Неймана). [Случай малых М см. в [3*] -Прим. ред.]

) Мизес Р., Математическая теория течений сжимаемой жидкости, ИЛ, М., 1961, § 25, п. 3.

§ 7. Парадокс Даламбера

картину. Еще более драматическим обстоятельством является то, что для некоторых профилей никакое околозвуковое течение без ударной волны невозможно. Этот парадокс околозвукового течения недавно установлен К. Моравец*). По терминологии теоремы 1, это означает, что задача околозвукового течения в теоретической (Эйлера - Лагранжа) гидродинамике может быть переопределенной.

В § 10 мы увидим, что задача сверхзвукового течения - типичная неполная задача, и примечательно, что различные разрешения парадокса обратимости в трех предыдущих случаях находятся в соответствии с общей математической теорией краевых задач эллиптического, смешанного и гиперболического типов.

§ 7. Парадокс Даламбера

Более известным и более давним, чем парадокс обратимости, является парадокс Даламбера. Согласно этому парадоксу, из допущений, сделанных в § 5, следует D = £ = 0. Для случаев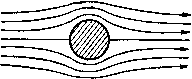

Рис. 1. Обтекание цилиндра, по Эйлеру.

кругового цилиндра (рис. 1) и сферы это следует, в силу симметрии, из явной формы потенциала скоростей:

и = а{х-\- (цилиндр). и=ах-\-~~ (сфера)

(12а) (126)

и теоремы Бернулли (8*) при g = 0. Если задача корректно поставлена, то наличие четырехкратной симметрии, как в данных случаях, позволяет показать, что D = I = О, исходя только из соображений обратимости (fl], стр. 248).

Вообще же парадокс Даламбера следует из принципа обратимости для любого профиля, который обладает центральной симметрией, т. е. для такого, который отображается в себя при

РР * Об), 45-68, 10 (1957), 107-131 и И

(1958). 129-144. [См. также [4*1, Ш-Прим. ред.]

отражении относительно неподвижного центра симметрии. Обтекание плоской пластинки на рис. 2, а дает пример подобного рода. Давления, действующие на элементы поверхности, соответствующие друг другу при центральной симметрии, равны по величине и противоположны по направлению. Следовательно, эта система сил сводится только к паре сил (см. прим. 1) на стр.26).

Разделяющаяся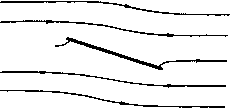

линия тона

Разделяющаяся линия тпна

Разделяющаяся линия тот

Рис. 2. Обтекание плоской пластинки, по Эйлеру (а), по Жуковскому {б) и по Гельмгольцу (s).

Демонстрация парадокса в общем случае дело довольно тонкое, при этом используется сложная теорема о поведении решений уравненияVf/ = О на бесконечности. А именно, пусть U(x) возрастает на бесконечности, по крайней мере как первая степень х = г. Тогда можно показать, что

i/=a.x+?(x),

где ф(х) «регулярна на бесконечности» ([4], гл. X, § 8; [2*]). Под этим мы понимаем то, что ф(х) можно разложить в некоторый