гии в расчете на элемент поверхности площади dS равна {[7], стр. 620, (9)) величине

-dE = py v]{%)dS, (50)

где Vt(yi) есть максимальная локальная тангенциальная скорость в течении Эйлера. Зная 0«(х), можно вычислить -Е и, следовательно, силу F, проинтегрировав выражение (50) по поверхности тела.

Так, если S - сфера радиуса а, то Vt(x) = (3/2) sinS. Интегрируя, получаем -Ё == Зтср Ууш/2 Следовательно, сила, действующая на сферу со стороны пограничного слоя, равна

Я=б1тр<у/=[-р.объем (S)](J)=9mS. (51)

Аналогичную формулу можно вывести для синусоидальных колебаний твердого тела произвольной формы ).

Применив к уравнению (48) преобразование Фурье, можно также вычислить результирующую силу в случае малого движения при любом его протекании в прошлом 2). Однако основной вопрос таков: применимы ли полученные таким образом фор-!чулы, и его мы сейчас рассмотрим.

§ 116. Колебания с большой амплитудой

Хотя часы с маятником сейчас имеют куда меньше значения, чем в 1800 г., однако было выполнено много опытов с тем, чтобы проверить правильность формулы Стокса (49) ). Очевидно, что .множитель присоединенной массы k и коэффициент затухания являются функциями как относительной амплитуды а, так и числа Стокса S. К сожалению, при свободном затухании величина а - переменная, и в большинстве опытов она не замерялась; по этой и по другим причинам значение многих опытов остается неясным.

Пожалуй, наиболее важными для случая больших амплитуд и малых S являются опыты Кейлегана и Карпентера") с ци-

) Lighthill М. J., Ргос. Roy. Soc. А224 (1954), 1-23.

-) Rayleigh, Phil. Mag., 21 (1911), 697-710; еще раньше такие формулы получили Boussinesq и Basset.

») Mever О. Е., 1. f. Math., 73 (1871), 31-68; North way М. Y.. М a с ken г i, Phys. Rev., 13 (1901), 145-164; McEwen Q. F., там же. 33 (1911), 492-511; Marty L., J. de Phys. et Radium fParis), 6 (1936), 373-382; Valensi J., Clarion C, Bull. Soc. France Mec, № 8; Richardson E. G., Та it R. I., Ost. Ing.-Archiv, 8 (1954), 200-207. Другие ссылки даны ниже и в § 103-104; см. также § 3!-32.

*) Keulegan G. Н., Carpenter L. Н., /. Res. Nat. Ви. Standards, 60 (1958), 423-440,

Сж = -тГ ад sin 9 Л (53)

Эмпирически было найдено, что для данных, полученных при колебаниях с большой амплитудой, вполне справедлива формула (52), когда эмпирические постоянные Со и См определяются по формулам (53) и (53). Измеренные значения постоянных Со

и См зависят в первую очередь от относительной амплитуды в = 2A/d и сравнительно мало ) - от числа Стокса 5. Графики измеренных значений Со и См изображены на рис. 28.

Интересно сопоставить формулу (52) с формулой, которая получается при стоксовых приближениях для малой амплитуды, т. е. с формулой

- Х{В) = с{х-+-т*х, пе = (т -\-т), (52)

) Когда а Э> 1, можно ожидать, что связь с «числом Рейнольдса»

Re = amd/v = a/2S будет иметь большое значение; см. Bagliarello - работу, цитированную в § 103,

линдрами И пластинками, помещенными в колеблющуюся жидкость. Полученные в этих опытах данные показывают любопытную зависимость присоединенной массы и затухания от относительной амплитуды, чего нет в формуле Стокса.

Пусть X = А sin обозначает зависящее от времени смещение, так что Г = 2тг/р есть период, 8 = - фаза и «щ = Лр - максимальная скорость. Сила Х{Щ измерялась как функция фазы; ввиду симметрии, Х(В + ж) --Х(Щ. Обозначим диаметр тела 2 через d, так что относительная амплитуда равна а = 2A/d.

Для измеренных значений функции J(S) оказалась подходящей полуэмпирическая формула

- Х(В)сх\х\ + Мх. (52)

В основе этой формулы лежит предположение, что сила -X (8) должна быть суммой силы лобового сопротивления D =

= ~ pdJcCn, пропорциональной квадрату скорости, и инерциальной силы Мх = (тср#/4)Сдгл:, пропорциональной ускорению. Если бы действительно было так, то Со и См можно было бы вычислять по формулам

Со = Г (6) COS 9 dB (53)

где т - теоретическая присоединенная масса, а масса вытесненной жидкости - то = р• объем {S). Для плоской пластинки, поставленной поперек течения, или для кругового цилиндра известно ([7], стр. 85), что т = В формулу (52) необходимо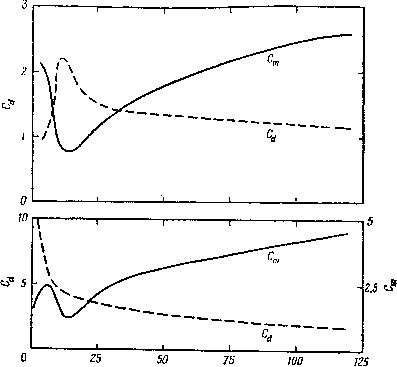

Рис. 28. Присоединенная масса цилиндра (вверху) и пластинки (внизу).

включить член то, так как препятствие удерживается неподвижным в колеблющейся жидкости; этого слагаемого не было бы, если бы препятствие колебалось в неподвижной жидкости. Эту разность можно вычислить, если учесть, что в системе жидкость постоянной плотности р и твердое тело при синусоидальных поступательных колебаниях всей системы на твердое тело S действует сила тох. Очевидно, что 1(9) не зависит от р.

Для сравнения были вычерчены также кривые значений См - для цилиндров и пластинок соответственно, - полученных