СВОДЯТСЯ К обыкновенным дифференциальным уравнениям. Однако имеются другие важные приложения метода поиска симметричных решений, когда задача сводится к уравнениям в частных производных. Наиболее очевидный пример представляют собой «конические течения» без осевой симметрии, которые впервые ввел и исследовал А. Буземан). Это - стационарные течения с полем скоростей (в сферических координатах)

u = u(cp, 6). (34)

Подобные течения получаются, например, около дельтавид-ных крыльев, так как такие крылья обладают конической симметрией.

Более аккуратное применение метода к расширяющемуся автомодельному течению необходимо при рассмотрении входа в воду клина или конуса с постоянной скоростью (см. рис. 25),

Твердый конус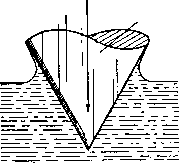

Рис. 25. Вертикальный удар конуса о воду.

причем скорость должна быть достаточно велика, чтобы на входе преобладали силы инерции. Сначала мы рассмотрим случай клина 2). Как и раньше, преобразование:

Xi->(j.Xi, t-xxt, величины р, р, щ не изменякутся (35)

оставляет инерциальную гидромеханику неизменной; мы даже можем считать жидкость сжимаемой! Поэтому метод «поиска симметричных решений» в случае клина предсказывает нам выбор решений вида

(36)

) См. NACA Tech. Memo. 1100 (1947) и данную там библиографию; см. также [10], § 10.5; Ф е р р н А., статья в книге Общая теория аэродинамики больших скоростей (ред. Сире У. Р.), Воениздат, 1962

") Этот вопрос был исследован Л. И. Седовым [14*]. - Ярил, ред.

U{x, у. 9; 0 = <T(-f. i).

т. е. одной единственной функции двух независимых переменных.

В случае несжимаемой жидкости теорию потенциала можно использовать для создания поля течения с помощью распределения источников на свободной поверхности, положение и интенсивность которых являются искомыми функциями одной переменной (длины дуги). Использовав эту идею, Шиффман и Спенсер ) показали, что условие постоянства давления на «свободной поверхности» приводит к системе интегральных уравнений относительно функций одной переменной. Значительным достижением, которое принадлежит Хиллману, было приближенное численное интегрирование этих уравнений для конуса с углом в 60°.

§ 89. Локальные и глобальные решения

Приведенные выше примеры показывают, что во многих случаях для задач, имеющих данную симметрию в пространстве и времени, существуют автомодельные математические решения. Однако сформулировать и доказать общую теорему существования гораздо труднее.

Когда имеется симметрия, достаточная для того, чтобы общие дифференциальные уравнения течения жидкости сводились к обыкновенным дифференциальным уравнениям, мы можем использовать стандартные локальные теоремы существования.

) Wagner Н., Zeits. ang. Math. Mech.. «2 (1932), 193-215. 2) Comm. Pure Appl. Math., 4 (1951), 379-417; в этой же статье изложены результаты Hi 1 m а п; см. также [17], гл. XI, § 9.

Этот метод сведения трех независимых переменных к двум использован в известной работе Г, Вагнера об ударе гидрЬплана при посадке на воду). Рассуждая, как в гл. III, § 2 мы можем свести задачу к функциям одной комплексной переменндй, но при этом усложнятся краевые условия.

Очевидно, тот же метод применим к задаче о конусе, входящем в воду с постоянной скоростью, и решение имеет вид

U(x, у, г; 0-<9(т- f • f)- (37)

т. е. мы перешли от четырех независимых переменных к трем.

В случае прямого кругового конуса, вертикально входящего в воду, задача имеет осевую симметрию и решение можно построить с помощью функции

•) ZAMM, 20 (1940), 186-198; см. также [15], гл. V § 4 н VII § 8. ) Наиболее аккуратное исследование проведено автором и Уолшем, Walsh J. М., Riabouchinsky Jubilee Volume, Paris, 1954, 1-12. a) Beran M., Quar. Appl. Math.. 14 (1956), 213-214,

Однако существование глобальных решений, удовлетворяющих соответствующим краевым условиям, предсказать гораздо труднее. Ярким примером встречающихся здесь трудностей может служить сжимаемое невязкое плоское течение с симметрией вращения (спиральные линии тока). Как впервые показал Ринг-леб), такое течение невозможно в «большом», поскольку его радиальная составляющая меняет свое направление на противоположное вдоль «предельной окружности».

Такую неопределенность наглядно можно продемонстрировать на течениях Тейлора - Маккола (§ 85), для которых режим конической симметрии типа присоединенной ударной волны ограничен условием достаточной малости угла при вершине конуса (при данном числе Маха). Для общего класса стационарных осесимметричных течений, удовлетворяющих уравнению (25), очень трудно строго определить существование решения в «большом», и опубликованные результаты не всегда надежны 2).

Подобным образом, хотя существование безударных центрированных волн разрежения возможно, волны сжатия связаны с ударными волнами, из-за чего весьма усложняется исследование существования решения в «большом» для автомодельных волн взрыва.

Другой интересный пример трудности определения глобального решения представляют собой осесимметричные струи (ламинарные, вязкие). Как показано в § 83, уравнения Навье - Стокса можно свести к обыкновенным дифференциальным уравнениям, если использовать автомодельное поле скоростей, имеющее в сферических координатах вид

u = r-f (б). (38)

К сожалению, как показал Беран), результирующее обыкновенное дифференциальное уравнение (17) не имеет глобальных решений, удовлетворяющих естественным краевым условиям для струи, вытекающей из круглого отверстия в плоской стенке или из какого-либо другого конического отверстия. Вопреки некоторым опубликованным результатам, по-видимому, только струя, вытекающая из труб с параллельными стенками, математически совместима в «большом» с требуемой симметрией (38) и естественными краевыми условиями.

Локальная теорема существования. Даже общие локальные теоремы существования нелегко доказать. Один