Оно легко интегрируется в замкнутом виде, причем качественно характер решений в адиабатическом случае i > 1 совершенно отличен от характера решений при т = 1, при - 1 < -у < 1 или при 1 = -1 (круговое течение).

В общем (неполитропном) случае уравнение (22) и соотношение с = ±g остаются справедливыми. В силу симметрии достаточно рассмотреть случай с = g. С помощью уравнения (21) мы получаем сначала Inр= фСс) = ф(), а затем уравнение

(+л+т()=о. (230

которое интегрируется численно ([14], раздел 7.1). (Если ё<{ё) = -1. то имеется особенность.) Следовательно, волны разрежения Прандтля - Мейера математически возможны для общего вида уравнения состояния.

§ 85. Конические течения Тейлора - Маккола

В пространстве п измерений (физически, разумеется, представляет интерес случай п = 3) уравнение неразрывности для стационарных осесимметричных течений принимает вид

О = (р/-"- со8-2ей,) + (рг-2 cos-2 бке) = = рг-г (со8-2ейэ) + [(« - 1) + рйз] /-«-2 cos-2 е.

Разделив все члены уравнения на выражение pr-2cos-2e и воспользовавшись соотношениями (19) и (20) (напомним, что уравнения (19) -(21) справедливы для пространственных течений), вместо уравнения (22) мы получим следующее уравнение:

(ft - 1) g - (« - 2) g tg О + g" -f g () = 0. (24)

Уравнение (21) в данном случае все еще справедливо, оно эквивалентно уравнению (21*) в политропном случае, и учитывая уравнения (21) и (21*), мы получаем соотнощение

Подставив это соотношение в уравнение (24), которое можно записать в виде

{Sf+g) + in- 2) (- g tg е + g) + g (-) = 0, (24)

§ 85. Конические течения ТвйлОра - Макко.га 171

МЫ получим следующий результат:

+ (n-2)(-gtg9-f-g) = 0. (25)

Последнее уравнение было численно проинтегрировано при Т= 1,408 (воздух) в известной работе Тейлора и Маккола [75].

Для баллистики (см. рис. 24) представляют интерес однородные и плоско-параллельные вначале течения, искажаемые затем конической ударной волной постоянной интенсивности, соглас-

Ударная волна

Конический снаряд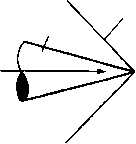

Р и с. 24. Коническое течение Тейлора . и Маккола.

но уравнениям Рэнкина - Гюгонио [также инвариантным относительно преобразований (18)]. Далее эти течения происходят в областях, где выполняется уравнение (25) ), пока они не становятся чисто радиальными (ff = 0), т. е. касательными к идеализированной конической головкеснаряда, полуугол при вершине которой равен р, а ось направлена по скорости невозмущеиного течения. Для заданных р, т уравнение (25) можно проинтегрировать численно при начальных условиях, а именно: задается ff(p) = О и любое значение безразмерного отношения g(i)/C в уравнении (21*). Имеется только одно значение угла ударной волны а и соответствующего числа Маха М, для которых уравнения Рэнкина - Гюгонио совместимы с плоско-параллельным движением вверх по течению от ударной волны. Поэтому мы можем записать а = а{М, р, i). Для заданных р, т такое решение с «присоединенной ударной волной» (ср. § 11) теоретически существует только при М>М(р, 7). Если М<М(р, i), то никакое коническое течение невозможно, и, следовательно, теория

) В случае плоскости линии тока в этой области - прямые (§ 84, случай I), иа что впервые указал А, Busemann, ZAMM, 9 (1929), 496-498.

) По поводу расходящихся плоских воли («центрированные волны разрежения») см. [6], § 46. О волнах давления, возникающих при расширении сферы, см. Taylor G. I., Ргос. Roy. Soc, А 186 (1946), 273-292.

») См. 162], [72] и [74]. О иих идет речь и в [57], гл. IV. В [57], гл. II, § 13, приводится ссылка иа более раннюю работу об автомодельных гравитационных волнах Н. Е. Кочина, Труды Мат. Института им. Стеклова, 9 (1935); см. также [7], п. 277.

предсказывает существование течения с «отошедшей ударной волной».

Подобные течения будут рассмотрены в § 88. Здесь достаточно отметить, что теоретически вычисленные границы конического режима, давление на коническую головку и угол присоединенной ударной волны (как функции числа Маха и угла при вершине конуса) ненамного отличаются от экспериментальных данных.

§ 86. Расходящиеся волны давления

Существуют также важные семейства нестационарных течений, обладающие внутренней симметрией (18). Из таких семейств особенно заслуживают упоминания расходящиеся волны- плоские, цилиндрические и сферические. Плоские расходящиеся волны возникают, например, когда в ударной трубе рвется диафрагма в области позади слоя взрывчатки, взорванного с одной из сторон, или позади поршня, который мгновенно начинает двигаться с постоянной скоростью в бесконечно длинном цилиндре). Сферические волны возникают при равномерном расширении сферы.

Интересно отметить, что с расходящимися волнами давления связано одно из первых сознательных применении метода поиска симметричных решений Мы рассмотрим их лишь с математической точки зрения.

Здесь удобнее перейти к переменным Лагранжа. Обозначим через а массу, определяемую путем интегрирования от какой-либо фиксированной материальной точки (например, от стационарного центра симметрии). Для плоских волн, если определять положение координатой х = f{a, t) и обозначать плотность через р = р(а, /), уравнение неразрывности эквивалентно соотношению а = дЦда между удельным объемом о = 1/р, величиной X и массой а. Поэтому допустимые для данного уравнения состояния p = Po~F{a) = Ро + *р течения соответствуют решениям уравнений движения. Последние сводятся к уравнению

W да -Т\да) 1? (26)