§ 55. Вихревые модели следов

В ОДНОЙ из старых моделей вводятся два симметрично расположенных за круговым цилиндром точечных вихря, как показано на рис. 23 (ср. рис. 13). Этой модели, которой мы обязаны Фепплю, уделялось значительное внимание ввиду ее чрезвычайной математической простоты, интересной теории ее устойчивости и связи ее с моделями вихревых дорожек (§ 56). Если вихри расположены на кривой 2гу = - ([у] стр. 155), где а - радиус цилиндра, то вихревая конфигурация находится в (неустойчивом) равновесии. Кроме того, можно добиться, чтобы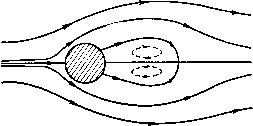

Рис. 23. Обтекание цилиндров, по Фепплю.

конфигурация линий тока модели имела хорошее согласование с наблюдаемой экспериментально, примерно в интервале 5 < Re < 30.

Однако вблизи центра вихря в стационарном плоском течении многие поля скоростей напоминают конфигурации линий тока в виде концентрических окружностей, и, следовательно, не стоит придавать слишком большое значение упомянутому согласованию. Теоретически же в стационарном течении завихренность должна из любого центра распространяться во внешние области, становясь асимптотически постоянной внутри любой замкнутой линии тока ламинарного течения при большом числе Рейнольдса.

Эта значительно более подходящая модель была недавно предложена Бэтчелором •), однако до сих пор при конкретных расчетах не удалось преодолеть вычислительные трудности. Кроме того, в виду неустойчивости по Гельмгольцу, реальные следы при больших Re дают в высшей степени нестационарное

) /. Fluid Mech., 1 (1956), 177-190 и 388-398; см. также Wood W. W., там же, 2 (1957), 77-87.

течение, и, следовательно, модель является нереальной. Для диапазона 5 < Re < 30, по-видимому, более приемлемой является модель вязкого течения Озеена (§ 31) )•

§ 56. Вихревые дорожки

Наиболее заманчивой вихревой моделью для следов является «вихревая дорожка», состоящая из двух параллельных рядов точечных вихрей, размещенных на одинаковом расстоянии, причем эти периодические ряды расположены «в шахматном порядке», так что вихри каждого ряда приходятся посредине между вихрями другого ряда. Эта модель была предложена Карманом") для представления периодических следов за цилиндрами, наблюдаемых в основном в интервале 30 < Re < 300. Для нее комплексный потенциал W = V + iV записывается в следующем виде:

1 Ig si" - g si" - f - А) } • (36)

Таким образом, потенциал включает три параметра: интенсивность вихря X, продольный размер а и поперечный размер Л. В любом конкретном случае определение этих параметров, очевидно, является основной задачей, а любой набор значений х, а и Л задает равновесное расположение.

Карман показал, что в невязкой жидкости такое расположение имеет неустойчивость первого порядка (т. е. отклонения от положения равновесия растут экспоненциально), если только Л/а не равно 0,281 (приближенно). Он показал также, что аналогичное размещение вихрей, при котором вихри в обоих рядах остаются параллельными [величина о/2 опускается в формуле (36)], всегда неустойчиво.

Кроме того, исследуя скорость К, с которой завихренность распространяется в пограничном слое по обе стороны, Гейзен-берг и Прандтль) получили соотношение

Kittmj, (37)

откуда x:=:i (1 + Q)av"/A. Хотя сам вывод весьма приблизителен, результат является надежным с точностью до множителя 2.

) Литература приведена в [17], стр. 263, примечание 13. Отличный исторический обзор вихревых систем в следах дал Розенхед Л., сб. Проблемы механики, ИЛ, М., 1955, стр. 446-454.

») Gott. Nachr., Math.-Phys. Kl. (1912), 547-556.

») Hei sen berg W., Phys. Zeits., 23, (1922), 363-366 и комментарии Прандтля на стр. 366; см. также [3], стр. 555, 564 и [11], т. 2, стр. 132.

§ 57. Количество движения в следе П5

Наконец, легко догадаться, что величина А не должна намного отличаться от диаметра цилиндра rf; в § 57 мы сможем в большей мере обосновать это теоретически. Учитывая все приведенные выше соображения, можно построить приближенную априорную модель периодических следов.

Очевидно, что эта модель вихревой дорожки возникла не из решения математической краевой задачи: остроумная идея Кармана не принадлежит к «рациональной гидродинамике» в смысле § 1. Так, в этой теории обтекаемое препятствие не является неким реально существующим геометрическим объектом.

Было высказано предположение, что вихревые дорожки естественно возникают при закручивании вихревых слоев, представляя, таким образом, асимптотические решения задачи Коши. Однако приближение в виде модели сосредоточенных точечных вихрей является нереальным как теоретически, так и экспериментально ), даже несмотря на то что, как иногда говорят, вихревые слои закручиваются, причем «завихренность все больше и больше сосредоточивается в закрученных участках».

Эти замечания имеют своей целью подчеркнуть, насколько далеко ушла современная гидродинамика от простой и догматической идеи Лагранжа. Все стационарные вихревые течения из § 55 и все решения задачи Гельмгольца удовлетворяют уравнениям Эйлера для несжимаемой невязкой жидкости; это показывает, насколько далека от «корректной» постановки задача стационарного течения для этих уравнений.

В действительности же само понятие «стационарного течения» ошибочно с физической точки зрения для жидкостей малой вязкости!

§ 57. Количество движения в следе

Однако тот факт, что идеи Лагранжа оказались ошибочными, не означает, что теоретический подход в гидродинамике следует отвергнуть. Как мы видели в гл. И, есть большие основания считать уравнения Навье-Стокса для несжимаемой жидкости заслуживающими доверия. Наше рассмотрение теории следов мы закончим кратким обзором результатов, полученных к настоящему времени при помощи этих уравнений. Как и в случае ка-витационного движения (§ 49), многое может быть объяснено при помощи законов сохранения.

Возможно, что наиболее полезной является интерпретация количества движения следа. В эксперименте позади всякого

) Теоретический разбор см. в работе Birkhoff G., Fisher Rend. Soc. Mat. Palermo, 8 (1959), 77-90, относительно экспериментальных данных см. [3], гл. XIII. Цитата взята из той же работы.