) См. Birkhoff G., Cay wood Т. Е., /. Appl. Phys.. 20 (1949), 646-659 (описание приборов, использованных в опытах, и другие снимки).

) См. [5], § 74 и указанную там литературу; а также Harvey Е. N.. The Military Surgeon, 98 (1946), 509-528.

) Теория гравитационных волн рассматривает тесно связанную с ней задачу, когда р = Ра на свободной поверхности. Обычно под поверхностью р>Ра, но в данном случае это условие не предполагается.

Несколько наиболее интересных фактов относится к кавернам позади снарядов, выстреленных в воду. Фото 1 дает нам отличный материал такого рода на фото показана каверна, образовавшаяся позади сферы, входящей в воду со скоростью около 45 ж/се/с. На одной и той же фотопластинке были сделаны два снимка со сдвигом во времени на 0,005 сек. Белые точки на снимках - это маленькие пузырьки, каждый из которых сфотографирован дважды. Нетрудно найти точки, соответствующие одному и тому же пузырьку, и длина вектора, идущего от первой точки ко второй для каждой пары, в грубом приближении пропорциональна вектору скорости воды вблизи пузырька. Таким образом, можно наглядно представить себе профиль каверны и поле скоростей течения.

Однако по разным причинам подобные снимки не вполне точно соответствуют теоретической постановке вопроса. Так, например, они изображают замедляемое тело, а не стационарное течение; поверхность воды является второй свободной границей, что усложняет математическое описание; к тому же нельзя пренебрегать влиянием воздуха (ср. § 53).

Применимость теории течений Гельмгольца качественно подтверждается тем, что позади снарядов, движущихся достаточно быстро, получаются каверны сколь угодно большой длины (100 диаметров и больше). Это явление имеет важное практическое значение: большое поражающее действие скоростных снарядов и осколков бомб обусловлено тем, что они могут проделывать отверстия, значительно превышающие их собственные размеры 2). Для нас же значение этого факта заключается в том, что он указывает физическое приближение к бесконечным кавернам, которые определяются математически как решения задачи Гельмгольца - Бриллюэна.

Обобщенная задача Гельмгольца. Если предположить, что выполняются условия (14) и что жидкость несжимаемая и невязкая, то можно применить концепцию Гельмгольца и к ускоренному течению с учетом гравитационных сил. С этой целью допустим, что кавитация самопроизвольно возникает, как только р < pv. Получающуюся таким образом краевую задачу можно назвать обобш,енной задачей Гельмгольца).

Идея о том, что реальную кавитацию можно математически описать при помощи рещений обобщенной задачи Гельмгольца, подтверждается качественным наблюдением того, что заполненные паром каверны возникают у твердых поверхностей. Это эмпирическое положение можно вывести при рассмотрении рб-общенной задачи Гельмгольца следующим образом). Применяя оператор Лапласа к уравнению Бернулли [гл. I, формула (5)], получим уравнение

V2/ = -PoV{yV£/Vf/+- + G}. (31)

Б формуле (31) V2G = 0, так как G есть ньютонов гравитационный потенциал; V(di/ldt) - d{VU)ldt = 0, в силу формулы (6) из гл. 1; и, полагая = л;, так что Vi/Vf/=2«ft. получаем формулу

V (2 ul) = 2 u,V4, 4- 2 2 • V«,) > 0.

Отсюда Vp < О, причем равенство имеет место только если u постоянная, т. е. р - супергармоническая функция. Известно, однако, что супергармоническая функция должна принимать свои минимальные значения на границе; следовательно, р будет становиться меньше pv прежде всего на границе.

§ 51. Пузырьки

Часто употребляемое вместо «каверны» слово «пузырек» указывает добавочно на малые размеры и подвижность. При рассмотрении маленьких пузырьков обычно необходимо учитывать силу тяжести и поверхностное натяжение, как мы уже видели в § 32. Мы изложим сейчас некоторые результаты относительно пузырьков, которые показывают правильность указанных соображений, и разъясним далее причины, по которым течения Гельмгольца дают лишь приближенную картину реальных каверн.

Сначала мы напомним ([11], т. I, п. 29) о скачке давления, равном 2i/r, который создается поверхностным натяжением i при переходе внутрь поверхности сферического пузырька радиуса г. Уже это беглое замечание указывает на возможность того, что жидкость, из которой удалены все пузырьки радиуса г > к, может выдерживать натяжение величиной (2j/r) -р„ без кавитации!

) Kirchhoff G., Vorlesungen uber Mechanik, 1876, стр. 186; см. также Bouligand G., /. tie Math., 6 (1927), 427,

Хотя ограниченность объема книги лишает нас возможности подробно исследовать этот увлекательный вопрос, мы все же напомним, что жидкости после дегазации в лабораторных условиях выдерживали натяжение величиной в десятки атмосфер), вопреки условию (14). Подобно этому вода, из которой удален воздух, может быть перегрета без парообразования. По этим причинам лабораторные измерения кавитации теперь, как правило, сопровождаются измерением содержания воздуха в жидкости. Только потому, что чаще всего «вода» не в достаточной мере однородна (ср. § 1), а содержит во взвеси много «пузырьковых ядер», условие (14) приближенно справедливо.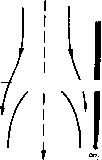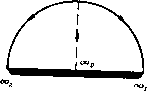

Рис. 21. Подъем плоского пузырька в канале.

Второй вопрос, имеющий математический интерес, связан с подъемом больших пузырьков в вертикальных трубах при наличии силы тяжести. Не затрагивая трудных задач физической реализации и устойчивости и пренебрегая поверхностным натяжением, мы рассмотрим идеализированный случай - подъем двумерного плоского пузырька, схематически изображенный ма рис. 21,0.

Наиболее интересно здесь большое сходство с математическими методами, введенными в § 45, 46. Чтобы показать это. снова отобразим течение на единичный полукруг Г в плоскости / (рис. 21,6), причем неподвижную границу отобразим на диаметр, а свободную -на полуокружность, как в § 37. Пусть d~ диаметр трубы и Uo - скорость подъема пузырька (если оси неподвижно связать с верхней точкой пузырька, то Uq есть скорость падения в ооо - в точке на бесконечности вверх по тече-

) С другой стороны, величина 250 атмосфер, которую часто приводят, является, по-видимому, неправильной; см. [17], гл. XV, §3.