§ 49. Законы сохранения

Контейнер

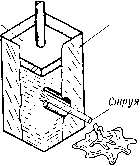Насадок Борда. Рассмотрим сосуд с вертикальными стенками, который заполнен жидкостью плотности р и в который вставлен насадок Борда с поперечным сечением произвольной формы и площади А (см. рис. 19); пусть давление на уровне насадка равно р. Мы предположим, что срыв течения ) с насадка происходит у его внутреннего края и что скорость струи, вытекающей из насадка, асимптотически приближается к постоянному значению v, которое представляет собой постоянную скорость на свободной линии тока, ограничивающей струю. Пусть А* - асимптотическое попереч- Поршет ное сечение струи; тогда, по определению, А*/А есть коэффициент сжатия. Мы подсчитаем его следующим образом.

Объем жидкости, вытекающий за единицу времени, равен vA*, его количество движения равно vA*; «расход» кинетической энергии составляет /грМ*. С другой стороны, добавляемое количество движения равно рА Рис. (избыточное давление), а энергия (потенциальная) равна

p{vA*). Отсюда рА = руМ* и pvA* = V2puM*. Разделив первое уравнение, умноженное на v, на второе, получим в результате равенство

4-= (29)

Кумулятивные заряды. Другое важное применение законов сохранения мы находим в теории направленных зарядов, которые использовались в американских «базуках», в британских PIAT и разных других видах противотанкового и фугасного оружия времен второй мировой войны. Мы здесь кратко изложим сущность подобного применения теории струй; дальнейшую литературу можно найти в работах [17], стр. 16 и [22*].

Конструкцию и действие такого оружия можно в принципе описать следующим образом. Взрывчатое вещество с металлической прокладкой окружает полую выемку; детонатор снаряда расположен в тыльной части. Рассмотрим только случаи конической и клиновидной металлической прокладки; в продольном

19. Истечение из Борда.

насадка

) Это случай «безнапорного течения»; см. Gibson А. Н., Hydraulics, Constable, London, 4-е изд., стр. 122; это условие не всегда выполняется.

разрезе они показаны на рис. 20. Взрыв заставляет прокладку двигаться внутрь и вперед, причем оказывается, что приведенная таким образом в движение прокладка обладает огромной пробивной силой. Чем объясняется появление такой силы?

Наилучшее из известных объяснений исходит из следующих правдоподобных допущений (приближенного характера).

Допущение I: получив начальный импульс от взрывчатки, стенки прокладки движутся внутрь под действием их соб-

Стент прокпадки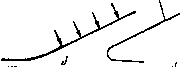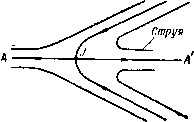

° б

Рис. 20. Схема действия кумулятивного заряда.

ственного количества движения с постоянной скоростью до тех пор, пока они не встретятся на «оси» (АА на рис. 20,а).

Допущение 2: под действием развивающихся при этом огромных напряжений металл прокладки ведет себя как идеальная жидкость.

Допущение 3: эта жидкость движется стационарно относительно осей, связанных с точкой / встречи противоположных стенок прокладки.

Допущение 4: поверхности стенок прокладки являются свободными границами.

Эти допущения сводят вопрос к задаче Гельмгольца о соударении струй (рис. 20,6). В плоском случае (клин) годограф представляет собой окружность; годограф же половины потока- полуокружность. Область W представляет собой бесконечную полосу с разрезом, поэтому можно полностью рассчитать течение) по методу § 37.

О [171, стр. 36; Щ стр. 283,

§ 50. КавитационнЫе течения как течения Гельмгольца ЮЛ

Для более важного случая конической прокладки мы не располагаем таким аппаратом. Однако с помощью законов сохранения все же можно приближенно указать зависимость скорости и массы струи от угла при вершине конуса и от используемой взрывчатки. Имея эти данные, можно оценить пробивную силу, пользуясь уравнением Бернулли ).

§ 50. Кавитационные течения как течения Гельмгольца

В § 43 было дано теоретическое обоснование эмпирического утверждения (Бетца - Петерсона, см. прим. 2} на :тр. 88), что теория струй применима, если р/р < 1- Это указывает на возможность математического описания кавитационных течений посредством решения краевой задачи Гельмгольца - Бриллюэна. Ниже мы дадим обзор доводов в пользу и против этого положения; в настоящем параграфе рассмотрим только первые доводы.

Во-первых, как и в случае кавитационных течений идеальной жидкости, очертания реальных каверн сравнительно гладкие, стационарные ) и имеют длину в 10 или более диаметров обтекаемого тела. Таким образом, они являются значительно лучшим приближением теоретической модели, чем реальные следы (см. § 53). Исключение составляют те случаи, когда препятствие помещено в кавитационную трубу при Q > 0,3.

Во-вторых, профиль каверны почти всегда выпуклый, и отрыв потока происходит у поперечного сечения с максимальным диаметром. Это утверждение в общем согласуется с решениями задачи Гельмгольца - Бриллюэна и заметно отличается от случая следов.

В-третьих, приближенная экспериментальная формула)

Се = 0.55+ 0,4Q = 0,55(1+0,73Q) (30)

для коэффициента Со при поперечном кавитационном обтекании цилиндра вполне хорошо согласуется с теоретическим значением Сх)(0) = 0,55, вычисленным Бродецким для задачи Гельмгольца - Бриллюэна по методу из § 46, если ввести поправочный множитель (1 + Q), согласно § 43*).

») Birkhoff G., MacDougall D. P., Pugh E., Taylor G., /. Aopl. Phys.. 19 (1948), 563-582.

) Если препятствие не совсем гладкое, могут возникнуть небольшие «биения», направленные по основному течению, как на фото I или в [23], стр. 116, 129. Когда Q > 0,3, каверна может попеременно вбирать и выпускать воду; см. [32], стр. 10.

•) Kempf Н., Foerster Е., Hydrodynamische Probleme des Schiffs-antrlebs. Springer, 1932, 227-342.

) Сопротивление цилиндра при различных числах кавитации было рассчитано рядом авторов, литературу см. в [17*]. - Прим ред.