Однако если предположить, что выполняется условие Бриллюэна (§ 43), то задача бесконечной каверны становится корректно поставленной, по крайней мере в некоторых случаях. Следуя Лерэ [35], определим «скобку» как препятствие Р, кривизна которого х(6) возрастает), как показано на рпс. 18.Лерэ доказал, что всякая симметричная скобка Р имеет единственную пару «точек Бриллюэна» Ао, Во, обладающих следующим свойством: кривизна свободных линий тока в точках отрыва Л, В при любом симметричном обтекании части Р равна --оо, конечна или равна -оо в зависимости от того, происходит ли от-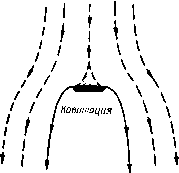

Р и с. 17. Обтекание плоской пла- Рис. 18. Обтекание «скобки» стинки, по Вилла. гольцу.

по Гельм-

рыв перед точками Ло, Во, в точках Ло, Во или позади точек Ло, Во соответственно. В первом случае ввиду бесконечной кривизны свободные линии тока должны проходить сквозь скобку, что невозможно. В третьем случае, очевидно, нарушается условие Бриллюэна. Следовательно, если мы определим задачу Гельмгольца - Бриллюэна, как задачу нахождения Эйлеровых течений, которые ограничены неподвижными препятствиями и свободными линиями тока, удовлетворяющими условию Бриллюэна, то получим следующее утверждение.

В случае бесконечной симметричной каверны позади скобки задача Гельмгольца - Бриллюэна поставлена корректно и отрыв происходит в точках Бриллюэна Ло, Bq. Интересно было бы точно определить класс симметричных препятствий, для которых задача Гельмгольца-Бриллюэна поставлена корректно.

Мы показали выше, что в случае скобок условие Бриллюэна эквивалентно условию конечности кривизны свободной линии

) По теореме о четырех вершинах, круг есть единственная «скобка», ограничиваюш.ая гладкую выпуклую область.

S 48. Осесимметричные течения Гельмгольца 99

тока. В литературе не раз встречалось утверждение, что последнее условие («гладкого отрыва» -см. работу [17], гл. VI. § 6) представляет собой «физически разумную» замену условия Бриллюэна. Однако в силу условий (14) и особенно в силу того, что при обтекании по Кирхгофу плоской пластинки нарушается условие «гладкого отрыва», условие Бриллюэна кажется нам предпочтительным).

§ 48. Осесимметричные течения Гельмгольца

Впервые осесимметричные течения Гельмгольца были строго математически проанализированы в 1946 г., когда Левинсон*) дал строгое исследование асимптотических очертаний каверны. Предполагая, что для них удовлетворяется условие

y = xg{x), где jirn=0. (27)

Левинсон доказал, что s = /г и что

С(1п;с)-"- <g(;c)<C(lnx)-

для некоторой постоянной С, при всех е > О и при достаточно больших X. Если условие (27) усилить до вида xg(x)lg(x) = = 0(1/1пдс), то можно получить соотношения

(28)

у~Сл:/.(1пл:)- (т. е. {jlm JlijnJ == const)

и лобовое сопротивление можно выразить по формуле

D = -!.

Однако Левинсон не доказал, что такие каверны существуют.

Первое доказательство существования конечных осесимме-тричных каверн было дано в 1952 г. Гарабедяном, Шиффером и Леви [24]. Пользуясь принципом Рябушинского о том, что свободные линии тока экстремизируют присоединенную массу относительно вариаций, оставляющих постоянным объем каверны, а также пользуясь новым результатом о том, что «симметризация» уменьшает присоединенную массу, эти авторы доказали существование осесимметричных течений Гельмгольца «типа

) См. также 12], § 5, где указанные вопросы впервые были рассмотрены с такой точки зрения.

, ») Lev ins on N., Annals ol Math., 47 (1946). 704-730. (См. также 117*]. -Ярил, ред.)

) Gilbarg D., /. Rat. Mech. Anal.. 1 (1952), 309-320 и SerrinJ. В., там же, 2 (1953), 563-575; см. также [17], гл. IV, § 12-14. Работу М. А. Лаврентьева см. в Математическом сборнике, 46 (1938), 391-458.

) По поводу анализа приближенных решений см. В i г к h о f f G., Symposium on Naval Hydrodynamics, August, 2.5-29, 1958 [32].

) Критические замечания по этой работе см. РФЖ «Механика», № 5, Б 309, 1963 г, - Прим, ред.

Рябушинского» (рассмотренных в § 44) для профилей произвольного очертания (и для любого Q>0). Существование же течений Гельмгольца с бесконечными осесимметричными кавернами не доказано детально, хотя показано, что это достаточно правдоподобно.

Единственность бесконечной осесимметричной каверны была доказана для препятствий с данной точкой отрыва Гильбар-гом и Серрином. Доказательство основано на методе сравнения, впервые введенном М. А. Лаврентьевым ).

Замечательным в указанных доказательствах является то, что в них используются существенно новые идеи. Это оказалось необходимым, так как аппарат конформных отображений, традиционно используемый в случае плоских течений, здесь уже не пригоден.

Любопытно также, что хотя существование и единственность плоских течений со свободными границами были доказаны более чем через 50 лет, после того как были построены первые нетривиальные примеры таких течений, мы до сих пор не знаем ни одного представляющего интерес аналитического («точного») осесимметричного течения Гельмгольца 2), и это несмотря на то, что мы располагаем теоремами существования и единственности.

Поэтому при анализе частных осесимметричных течений Гельмгольца приходится опираться на приближенные методы. Из применявшихся до сих пор методов наиболее остроумным является метод разложения по степеням числа подобия, разработанный Гарабедяном [25] з). В то время как предыдущие ав-горы получили для коэффициента сжатия струи, вытекающей из круглого отверстия в плоской пластинке, величину 0,61, вычисления Гарабедяна привели к результату 0,58.

§ 49. Законы сохранения

Математические доказательства результатов, сформулированных в § 48, крайне сложны. Полезные результаты относительно осесимметричных течений Гельмгольца часто можно получить гораздо проще, обращаясь к физическим законам сохранения, как это и будет сделано ниже.