) В задней части каверны за осесимметричным препятствием может образоваться также пара вихрей с пустой внутренней областью ([42], стр. 230).

») См. работу [17], гл. V, § 10, 14, а также работу [2]. стр. 58. [Случай заостренной каверны перед пластинкой был рассмотрен С. А. Чаплыгиным еще в 1899 г. [18*]. Задача о заостренной каверне зэ обтекаемым клином также была решена С. А, Чаплыгиным [19*]. - Прим. ред.]

Время от времени и неустойчивы). Поэтому модель возвратной струи представляет особый интерес с физической точки зрения.

Позади выпуклых тел можно построить также «заостренные» каверны при Q < О, хотя в свое время считали, что это невозможно*). Однако такие каверны вовсе не похожи на наблюдаемые, образцы которых показаны на фото I и фото И (см. § 51). Сохранить повышенное давление в устойчивой каверне (или в следе конечной длины), по-видимому, очень трудно.

§ 45. Криволинейные препятствия

Для математического аппарата, описанного выше, существенно то, что нам известны специальные конформные отображения и интегралы от специального вида функций. Хотя этот аппарат тщательно разработан и пригоден для решения многих задач с полигональными препятствиями (см. (17], гл. И, III и V), он, вообще говоря, не пригоден для исследования кавитационного обтекания криволинейных препятствий.

Создание быстродействующих вычислительных машин дало возможность подойти по-другому к этой проблеме, пользуясь обиими теоретико-функциональными методами. Хотя такой подход до сих пор успешно применялся лишь к плоским течениям и хотя ниже мы будем рассматривать только такие приложения, подобные методы вполне могут быть применимы к осесиммет-ричным и даже к произвольным струйным течениям.

В качестве иллюстрации этого современного подхода мы рассмотрим общий случай криволинейного препятствия, симметрично расположенного в бесконечном потоке, как показано на рис. 16. Мы снова будем предполагать, что смачиваемый участок АСВ поверхности препятствия расположен вертикально, и выберем единицы измерений так, чтобы на свободной границе было выполнено условие 1 = 1.

Следуя Леви-Чивита [33], отобразим конформно и однозначно односвязную область течения на внутренность полукруга Г:

\t\<\. Im{}>0. (17)

§ 45. Криволинейные препятствия 93

Из основной теоремы о конформных отображениях) следует, что имеется в точности одно такое отображение t <= f(z) области течения на внутренность полукруга Г, переводящее точки А, В, С соответственно в точки 1, -1, /. Очевидно, что функция /(г) отображает свободные линии тока на диаметр, расположенный на действительной оси, а смачиваемый участок поверхности препятствия- на полуокружность t = е<(0 <о< i:). (В этом случае мы используем обозначения, отличающиеся от § 38-40.)

Чтобы получить выражение для комплексного потенциала.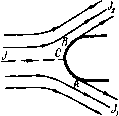

Рис. 16. Обтекание криволинейного препятствия.

удобно отобразить область Г на верхнюю полуплоскость посредством конформного преобразования

Т =--Y- так что-5 =--2- 08)

Тогда комплексный потенциал, очевидно, задается так:

W=. ~ = МТ. Ж>0, (180

где М - некоторая положительная постоянная. Это следует из того, что формула (18) позволяет отобразить область течения на плоскость с разрезом, причем точка разветвления / = i попадает в точку W=T = b, а точка на бесконечности / = 0 -в точку Г = со.

Теперь рассмотрим функцию {i - t)/(i + t) = {I + it)/(l-it). Модуль ее равен единице, если f - действительное число;

ее аргумент на участке АС равен 11/2, на участке СВ равен

) В 1 е b е г b а с h L., Lehrbuch der Funktlonentheorie, Springer, Leipzig, 1923, T. 1, стр. 61. По поводу принципа отражения Шварца см. там же, стр. 225. [На русском языке см., например, Маркушевич А. И., Теория аналитических функций, ГИТТЛ, М.-Л., 1950; или Лаврентьев М. А., Ш а б а т Б. В., Методы теории функций комплексного переменного, М,-Л., - Прим. перев.]

1 = С1 =

1-«

е<)=т(0. (19)

Поэтому функция i{t) обращается в нуль на диаметре полукруга Г, т. е. функция Q(t) действительна, когда действительно t.

По принципу симметрии Шварца (см. прим. 1) на стр. 93) функцию Q{t) можно аналитически продолжить на внутренность единичного круга \t\<l. Поэтому в рассматриваемом нами симметричном случае ( и iQ(f) действительные на мнимой оси t, являющейся осью симметрии) мы можем написать равенствд

Qit) = a,t-\-aJ-a,t+ (20)

где все at действительные числа, причем радиус сходимости ряда (20) не меньше единицы. Для неподвижной границы / = 1 с помощью довольно тонких рассуждений можно доказать, что функция Q{t) даже непрерывна ([17], гл. VI, стр. 135). Не строго выражаясь, множитель {I - it)/{I + it) «снимает» простой полюс для функции (нуль для функции S) в критической точке.

Обратно, для данной функции (20) с радиусом сходимости, равным единице или больше единицы, уравнения (19) и

- = /-()()--т/-(<-гV (2.)

определяют течение, разделяющееся на две симметричные части

позади гладкого препятствия АСВ. имеющего непрерывную касательную. Это приводит к классическому результату Леви-Чивита.

Теорема 1. Течениям, разделяемым на две симметричные части симметричным препятствием в бесконечном потоке, однозначно соответствуют различные функции вида (20), регулярные при / < 1 и непрерывные при \t\ = I, и постоянные М. Это соответствие задается уравнениями (19), (20) и (21).

-11/2, В точке С имеется скачок аргумента -и. Новая функция Q{t) = б + И, определенная формулами

также аналитическая и регулярная функция внутри области Г. На свободной границе, где f - действительное число, имеем равенство \\ + it\ = \\ - it\, и следовательно, можно записать соотношение

\ + it