§ 40. Влияние стенок

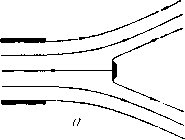Это опять-таки следует из того, что область W ограничена линиями тока, на которых V = const, включая линию тока, разделяющуюся в критической точке. Область годографа ограничена свободными линиями тока, на которых величина С постоянна, и неподвижной пластинкой, вдоль которой величина Z, направлена вертикально.

С математической точки зрения удобно так выбрать начало координат и единицы измерения, чтобы область W представляла собой полосу -%<V< U, разрезанную вдоль положительной полуоси W = = и > О, а область годографа-полукруг ю < \,-<

<arg?<.

Удобно также рассматривать только нижнюю половину течения.

При этих условиях область значений Т = е совпадает с полуплоскостью. Так как преобразование l отображает половину области годографа на единичный полукруг 0<arg?;< < тс, 11 < 1, то функция (2 + -2)/2 отображает ее на полуплоскость. В силу основной теоремы о единственности конформного отображения, отсюда следуют соотношения:

W=\n Т, а(сЧГ2)--26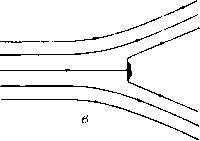

(10)

Рис. 12. Примеры плоских течений.

а - пластинка в струе, вытекающей из сопла; б -пластинка в канале; в -пластинка в свободной струе.

где величины а, Ь, с, i - действительные числа. Эти действительные постоянные можно связать с геометрическими свойствами течения. Если v < 1 - скорость течения в сопле (предполагаемая постоянной) и е""-скорость в нижней струе, то £ = у,

= 21п

Используя формулы (12а), (126), можно показать, что поправка на влияние стенок для коэффициента Со мала, если ис-ходить из скорости на свободной линии тока, но она очень велика, если исходить из скорости вверх по течению. Так, она составляет 30%, если (двумерный) туннель имеет ширину в 100 диаметров. В случае свободной струи эта поправка мала, и рассмотренная выше проблема не возникает.

§ 41. Неустойчивость течений Гельмгольца

К сожалению, свободные границы струй и следов, рассмотренные Гельмгольцем и Кирхгофом, неустойчивы. Это было известно уже Гельмгольцу ([27], стр. 222), который заметил, что границы струй, вытекающих из духовых труб, закручиваются в виде периодических спиралей.

Кроме того, наблюдения показывают, что при числах Рейнольдса Re > 10* линии тока, которые отделяются от плоской пластинки (или другого препятствия) в движущемся потоке, вскоре прекращают свое существованне в турбулентной «зоне смешения». Вследствие этого реальный след никоим образом не представляет собой неподвижную полосу «мертвой воды», простирающуюся в бесконечность, как полагал Кирхгоф. Реальные следы заполнены вихрями, которые наиболее активны

) Задачи, рассмотренные в f 40. впервые были решены в 1890 г.

Н. Е. Жуковским [15*]. - Прим. ред.

когда W = -оо и Г =1 = О, в то время как t =" в», когда W = Т ао. Таким образом, отбрасывая постоянные слагаемые, получим следующее выражение:

W=]n [(" - e") -в-")1 - 1п КС» - -и») (С» - -»-»)] -

= 1п[С*-2СС2Ч-11 -InIC* -(х; + г»-2)С»+11, (11)

где С = cos 2а. Поскольку из формулы (2) 2 = J С~ dW, это

выражение можно проинтегрировать элементарным способом и получить z() в замкнутом виде).

Особый интерес представляют случай С = 1 - пластина в закрытом канале (рис. 12,6), для которого можно получить соотношение

2 = 4 arc th С-2x1 arc th - - arc th , (12а)

и случай 0=1- пластина ширины v в свободней струе, (рис. 12,в), для которого можно получить соотношение

§ 41. Неустойчивость течений ГельмгоЛьцй 85

в зоне смешения, и эти вихри непрерывно выносят жидкость вниз по течению за пределы следа.

Чтобы объем жидкости, образующей след, оставался одним и тем же, необходимо, чтобы в центре следа поддерживалось обратное течение. В результате этого в потоке появляются два вихря, как это изображено на схеме рис. 13. Эти вихри поддерживаются значительным градиентом давления, они намного уменьшают давление p„ в кильватерной зоне позади пластинки.

Ввиду такой крайней неустойчивости в реальных следах получается значительное понижение давления: давление в них р«,

Зона

смешения

Рис. 13. Обратное течение в реальной следе.

гораздо меньше давления ра в смежных областях. Как следствие этого найденный Кирхгофом теоретически коэффициент сопротивления Сц = 0,88 меньше, чем половина действительного значения Со, которое приблизительно равно двум. Для наклонных пластинок значение подъемной силы Сь в модели Кирхгофа занижено даже в большей мере, особенно при углах, меньших «критического угла» (около 15°).

Если бы это было не так, то полет самолета был бы крайне затруднен. Это заметил Рэлей ([12], т. I, стр. 287, и т. III, стр. 491) уже в 1876 г. К счастью, модель Жуковского из § 8 является гораздо лучшим приближением действительной картины при малых углах атаки. (Кроме того, отрыв потока можно намного задержать при помощи соответствующей конструкции крыла, как уже было объяснено в § 29.)

Эти факты были хорошо известны Кельвину), который получил более важный результат: он показал, как можно количественно исследовать устойчивость прямолинейных линий тока в плоскопараллельном течении.

Очень большой интерес представляет случай горизонтальной границы в вертикальном поле силы тяжести. Граница разделяет две жидкости с плотностями р и р, которые движутся соответственно со скоростями и и и, как указано на рис, 14. Кельвин показал, что в этих условиях синусоидальное возмуще-

) Nature. 50 (1894), стр. 524, 549. 573; см. также Рэлей [Щ, т. в, стр. 39