при вершине равным тс/п ([17]), гл. II). В этом случае преобразование " отображает область годографа на полукруг и, следовательно, соотношение

~ f (--f l)-f 2dC

представляет собой отображение области годографа на полуплоскость. А дальше мы действуем, как в предыдущем случае.

§ 38. Истечение струи из щели

Гельмгольц [27] первый применил в 1868 г. описанный выше аппарат к случаю плоской струи, вытекающей из щели, см. рис. 11, а. В этом случае, выбрав единицу длины так, чтобы скачок V при переходе через отверстие был равен тг, мы можем в формулах § 37 положить W = 1п 7", 7" = е. dW/dT = 1/7".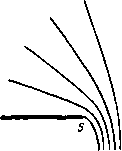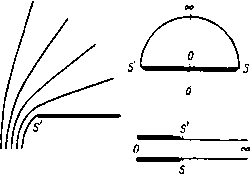

Рис. 11. Плоская струя, вытекающая из щели.

Для выбора величин а, Ь, с, d рассмотрим зависимость между 5 и W в физической плоскости. Очевидно, что предел = О в области годографа на рис. 11,6 достигается тогда, когда W => = -оо в области W на рис. 11, в или, что эквивалентно, когда 7 = 0. Из этого следует а = О в формуле (3). С точностью до подобия мы можем теперь написать равенства

W=\nT, C-dlc. (5)

С» -2CC-f 1

Точка струи, лежащая на бесконечности, где 47 = -Ь оо, очевидно, соответствует значению £ = е"», (С + С")/2 = о = С =

§ 39. Схема обтекания Кирхгофа 81

= cos а. Следовательно, уравнения (2) и (5) определяют струю, вытекающую из щели в бесконечной пластинке и образующую с этой пластинкой угол а. Так как подинтегральное выражение в формуле (2) представляет собой рациональную функцию, мы можем произвести интегрирование в замкнутом виде и получим, учитывая равенства (5), следующее соотношение:

1Г=1пС-1п(С2-2а+1); (6)

детали вычислений мы здесь опускаем. Случай вертикальной струи, рассмотренный Гельмгольцем, соответствует С = cos а = 0.

§ 39. Схема обтекания Кирхгофа

В 1869 г. Кирхгоф [31] выполнил аналогичные расчеты для следа позади пластинки. В этом случае преобразование W = = отображает нижнюю полуплоскость на плоскость с разрезом, являющуюся областью W\ таким образом, R{T) = 27" в формуле (4), если направить действительную ось вдоль пластинки.

Для того чтобы определить постоянные а, Ь, с, d в формуле (3), мы снова рассмотрим зависимость между W я t, в физической плоскости. Точка W = О, в которой начинается разрез, соответствует критической точке течения, в которой 1 = 0. Отсюда а = О, и мы снова можем написать равенства (5), помня при этом, что С = cos а определяет направление течения на бесконечности.

Наиболее интересен случай обтекания пластинки под прямым углом; он представляет собой плоское течение, аналогичное изображенному на рис. 10,6. В этом случае равенства (5) сводятся к виду

Выполняя интегрирование, указанное в формуле (2), мы на этот раз получаем следующее соотношение:

г=-(с4тР+{сЧ~Т>"ТТт}+°"5* (8)

для всех значений ? = -Ь щ.

Вдоль пластинки величина принимает действительные значения и соотношение (8) сводится к виду

г = -(тр- + т{1+arctgC}. (8а)

§ 40. Влияние стенок

Метод годографа 3) можно также применить с целью получения информации относительно влияния стенок на струю при истечении из сопла.

Рассмотрим, по Гельмгольцу, обтекание пластины, половина ширины которой равна Ь и которая удерживается в симметричном положении в струе из сопла, как показано на рис. 12, а. Так же как и раньше, функции W(z) и %{z) конформно отображают течение на бесконечную полосу с разрезом и на полукруг соответственно.

) Автор предполагает, что плотность жидкости равна единице.- Прим. ред.

) Через Cl обозначен коэффициент подъемной силы. - Прим. ред, ») См. I17J, гл. 11, § 7. 8; а также гл. 1, § 11.

где, очевидно, 2(0) = О, и, таким образом, постоянная интегрирования равна нулю. В правой точке отрыва 5= 1, следовательно.

Давление легче всего вычислить, положив ? = i = tg6 вдоль пластинки, так что ?/( + 1) =sin6-cos6= l/2sin26. Следовательно, в силу теоремы Бернулли) и формулы (8а), давление на пластинку равно интегралу

1 1 It/4

i\-\)dx= Jlillrf[sin2 29]= / 2cos229rf6=.

Отношение этой величины к половине длины пластинки, очевидно, представляет собой коэффициент лобового сопротивления, который, таким образом, равен величине

Cd== = QM. (9)

Аналогичные, но более сложные подсчеты для случая обтекания пластинки под острым углом а, Ф позволяют получить следующие формулы 2):

2я sin а ж sin 2g