§ 36. Разрывные течения

условие равновесия на линии тока, являющейся линией разрыва,-это непрерывность давления при переходе через нее.

Если линия тока ограничивает идеалязированный след или какую-либо другую область, заполненную неподвижной жидкостью («мертвая вода»), а сила тяжести учтена согласно теореме 1 из § 21, то условие непрерывности давления равносильно условию постоянства давления в рассматриваемой области. Поэтому ввиду непрерывности давления на линиях тока, ограничивающих след. давление должно быть постоянным. Линии тока, на которых скорость изменяется скачком, а давление постоянно, называются свободными линиями тока.

Разделяющаяся п линия пюка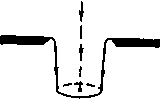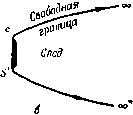

Р и с. 10. а - круглая струя; б - след позади диска.

В силу уравнения Бернулли (8*) гл. I, если все еще пренебрегать силой тяжести, скорость остается постоянной вдоль любой свободной линии тока при стационарном течении, и наоборот: vdv = -dp/p = 0. Это дает чисто кинематическое краевое условие для стационарных течений, ограниченных свободными линиями. Вместе с формулами § 5 оно определяет следующую краевую задачу теории потенциала.

Задача Гельмгольца. Для заданного препятствия R найти потенциал скоростей, удовлетворяющий 1) уравнению VU = О вне препятствия R и вне области «мертвой воды» Ru 2) условию ди/дп = О на границах препятствия R и области R\ и 3) условию I = const на границе области R\.

Заметим, что последнее краевое условие нелинейно. Заметим также, что топология течения осталась неопределенной; на практике ее задают исходя из интуитивных представлений или экспериментальных данных (гипотеза (D) из § 1). Две такие топологии течения схематически изображены на рис. 10. На этих рисунках показаны «струя», вытекающая из круглого отверстия в плоской стене, и «след» за диском.

Течения, удовлетворяющие указанным условиям 1)-3), т.е. решения задачи Гельмгольца, в последующем мы будем называть течениями Гельмгольца.

В действительности же никто еще не сумел дать точную математическую трактовку указанных выше двух течений Гельмгольиа, см. § 49. Однако аналогичные течения для плоского случая, т. е. струя, вытекающая из щели, и след позади плоской пластинки, можно построить довольно легко. Теория этих плоских течений Гельмгольца будет предметом исследования в § 37-39).

§ 37. Годографы в виде полукруга

В общем случае локально безвихревые несжимаемые плоские течения характеризуются существованием комплексных потенциалов W = и + iV. Здесь U - потенциал скоростей, а V ~~ функция тока. Комплексный потенциал W есть аналитическая функция комплексной переменной z = х + iy, характеризующей положение точки, а ее производная

dW . . ...

- = = a~tv (1)

представляет собой сопряженное значение комплексной скоро-

сти2) и-\-IV = 1*, гяе и = -. v = -.

Если известен потенциал W=f(t,) как комплексная аналитическая функция 5, то, следовательно, можно определить z в виде аналитической функции от т. е.

z = fCf{qd(. = jCdW, (2)

и следовательно, можно (в принципе), исключив С, найти W{z). Итак, для определения стационарного плоского течения Гельмгольца достаточно знать функциональное соотношение W =/(С). Каков вид этой функции в случае плоских течений, приведенных на рис. 10, можно догадаться по годографам рассматриваемых течений.

Годографом плоского течения называется геометрическое место тех значений , которые действительно достигаются в этом течении. Из рис. 10 легко видеть, что годографы соответствующих плоских течений (если они существуют) должны быть полукругами. Это следует из того, что arg (направление течения) - величина, постоянная на плоских пластинках (фиксиро-

) В русской литературе принят термин «теория струй», в эту теорию входит изучение всех течений со свободными поверхностями, на которых давление постоянно. - Прим. ред.

) В русской литературе комплексной скоростью называется сама величина dw/dz = и - iv. - Прим. ред.

§ 37. Годографы в виде полукруга 79

ванных границах), в то время как (скорость течения) постоянна вдоль свободных границ, как показано в § 36.

С другой стороны, область или геометрическое место значений, принимаемых в данном течении величиной W, ограничена линиями V = const (линии тока), параллельными действительной оси и. На рис. 10, а -это бесконечная полоса. Для случая на рис. 10, б -это полуплоскость, разрезанная вдоль положительной оси и (если выбрать постоянную интегрирования в

W=dz так, чтобы ft критической точке было W = Q).

Аппарат конформного отображения. Пусть теперь Ф - любое течение, имеющее годографом полукруг (следовательно, ограниченное свободными линиями тока и прямолинейными стенками). Мы можем так выбрать оси координат, что величина будет принимать действительные значения на неподвижной границе, и так выбрать единицы измерения, что на свободной границе будет g = 1. Затем с помощью преобразования о = ( -f -•)/2 отобразим область годографа на нижнюю полуплоскость lm{a}<0. Конформное преобразование наиболее общего вида, отображающее область годографа на нижнюю полуплоскость, задается формулой

где а, Ь, с, d - действительные числа.

С другой стороны, область W любого односвязного течения, ограниченного линиями тока, есть обобщенный «многоугольник», одна или большее число вершин которого расположены на бесконечности и все стороны которого параллельны действительной оси. Следовательно, можно отобразить область Т, определяемую соотношением (3), на область W при помощи подходящего (конформного) преобразования Шварца - Кристоффеля:

где С и Bj, Th~действительные параметры ([4], стр. 370). Мы видим, что для любого односвязного течения Ф, у которого область годографа есть полукруг, можно записать W в виде

1*(0, используя формулы (3) и (4), где А {I) - рациональная функция.

Рассмотренный выше метод можно легко обобщить на случай, когда область годографа есть круговой сектор с углом,