§ 17. Парадокс тройной ударной волны

В § 14 упоминалось о том, что уравнения Рэнкина - Гюгонио выводятся из законов сохранения. Эти уравнения показывают, что в случае совершенного газа отношения давлений, плотностей и температур р/р, р/р, Т/Т по разные стороны от стационарной ударной волны зависят только от одного параметра (интенсивности скачка или числа Маха - см. [15], гл. IV, § 4). Кроме некоторых исключений, от.меченных в конце § 14, эти выводы подтверждаются экспериментально, причем на практике можно наблюдать ударные волны различной силы.

Не так обстоит дело с «кратными» ударными волнами. В случае двойной, «регулярно» отраженной ударной волны (см. рис. 6, а) и тройной ударной волны, или F-волны Маха (см.

Отраженная

Падающая

Отраженная

Падающая

Течение скольжения

Отраженная

Падающая Отраженная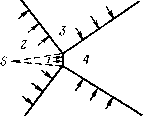

Падающая

Рис, 6. Отражение ударных волн.

~ регулярное отражение; б - К-образное отражение но Маху.

рис. 6,6), соответствующие математические расчеты возможны, если предположить, что в каждом из получающихся при этом секторов (1, 2, 3, 4) физические переменные принимают определенные предельные значения вблизи особой точки в «вершине» ударной волны. Многие из таких расчетов также подтверждаются экспериментально, так что эта теория является весьма правдоподобной.

Однако в случае «слабых» ударных волн регулярные отражения происходят при углах падения несколько больших, чем это допускается теорией, а полученные при расчете предельные значения для тройных ударных волн значительно отличаются от

§ 18. Значение уравнений Эйлера 45

наблюдаемых. Это противоречие, которое можно назвать парадоксом тройной ударной волны, было, по-видимому, открыто Дж. фон Нейманом (1945 г.).

Не раз пытались разрешить этот парадокс, который, возможно, является «парадоксом особой точки», т. е. получается из-за чрезмерно упрощенной картины локального поведения вблизи особой точки. Но до сих пор не дано ии одного удовлетворительного истолкования )•

§ 18. Значение уравнений Эйлера

Предыдущие парадоксы показывают, что область применимости уравнений Эйлера имеет некоторые ограничения; однако эти уравнения все еще являются основным орудием практической гидромеханики. Так, они дают возможность приближенно вычислить: 1) распределение давлений на лобовой поверхности препятствий; 2) подъемную силу крыла самолета; 3) силы при движении с «кавитацией» (гл. III) и наличии струй; 4) гидродинамическое противодействие ускорению твердого тела в жидкости («присоединенная масса», см. гл. VI); 5) распространение гравитационных волн, включая сейши, приливы и отливы; 6) распространение звука (акустика); 7) распределение давления и скорости течения в сверхзвуковых соплах и 8) сверхзвуковое лобовое сопротивление.

При подобных расчетах необходимо иметь в виду описанные выше парадоксы, а также большое разнообразие течений, удовлетворяющих теории невязкого обтекания при наличии завихренности. В теоретической гидродинамике это разнообразие иногда как бы остается в тени из-за того, что слишком много внимания уделяют теоремам существования и единственности кстати сказать, при доказательстве таких теорем часто исходят из нереальных допущений. Это подчеркивается в большинстве книг по «современной гидродинамике» (например, в работах [3] и [24]), где с самого начала указывают, что возможна неоднозначность решений, а также отмечают такие удивительные экспериментальные явления, как пограничные слои и турбулентность.

Однако наличие таких обстоятельств вовсе не должно снижать значение чисто математической теории невязких жидко-

го, Bleakney W. and Taub А. Н., Revs Mod. Phys.. 21 (1949)

587-605; [6], стр. 342; [15], стр. 144; Р о 1 а с h е к Н. and S е е g е г Y(, Phys

Ивп Я4 /1Q[1\ ПОП поп „ Г1г * > у •

стей. Теория в состоянии указать существенные возможности, которые «здравым смыслом» были бы отвергнуты как абсурдные.

Например, теория указывает, что могут быть крылья с пренебрежимо малым лобовым сопротивлением. Хотя этот идеал пока еще не достигнут, он явился стимулом для многих важных работ (см. § 29).

Наконец, из парадокса обратимости следует возможность того, что область «мертвого» воздуха, или «след», может образоваться впереди цилиндра. Наличие такой области сделало бы возможным обтекание конечного цилиндра таким же потоком, как и известное обтекание Тейлора - Маккола (§ 85) для конического снаряда. Такое течение характеризуется тем, что на боковой поверхности конуса всюду постоянное давление. Согласно теории «следов» (гл. 1П), твердый конус можно было бы, не нарушая равновесия, заменить идеальным невязким воздухом при постоянном избыточном давлении. Математически это означает, что в идеальной жидкости возможно обтекание плоского диска сверхзвуковым потоком, при котором невидимый конический воздушный барьер защищает диск от давления воздуха, намного уменьшая лобовое сопротивление.

Здравый смысл и интуиция немедленно отвергают возможность подобного течения как до нелепости неустойчивого. Логическая основа здесь такая же, как и в том случае, когда отвергают возможность существования «следа» в области вверх по течению. Кажется в высшей степени правдоподобным, что наличие препятствия дает себя знать лишь в области, расположенной вниз по течению ).

И все же в данном случае, по-видимому, скорее ошибается здравый смысл, чем математический вывод! Снимки, сделанные в Абердинской научно-исследовательской баллистической лаборатории (см. фронтиспис), показывают, что очень тонкая игла, помещенная перед диском, действительно способна создать нечто вроде подобного «абсурдного» течения.

Ввиду этого и других примеров мы считаем, что у математиков нет оснований думать, будто в гидродинамике снижается значение дедукции (при сопоставлении ее с «физическими выводами»), если учитываются те гидродинамические парадоксы, которые выявились в эксперименте.

) Те же самые интуитивные догадки были использованы в § 10, чтобы выделить более предпочтительное «простое обтекание» тонкого крыла.