Алгоритм для задачи распределения Р. Силвер (Silver R. «САСМ», 1960, № 11)

Аннотация. Формулируется и кратко излагается зада-ча распределения. Для ее решения на языке AJIFOJI представлен эффективный алгоритм. Дается эмпиричес-кое соотношение между временем решения и объемо]у1 задачи, основывающееся на обширных экспериментах, проведенных на .вычислительной машине.

Задача распределения. Эта задача может быть сформулирована следующим образом. Дана матрица {йг, j) размерности w.X«. Найти перестановку л; целых чисел 1, 2,такую, которая минимизирует сумму

2 j. , т. е. для любой перестановки у целых чисел «=1

1, 2,имеем 2 г.лг.З .i * t=i г=1 *

Задача распределения получила свое название от следующего цримера.

Пример. Каждый из п человек Mi,М п должен быть распределен на работу из множества Л,..., /„ работ по одному человеку .на каждую работу. Для каждой пары «человек-работа {Мг, Ji)» имеется количественная оценка di,j производительности человека на работе. Найти такое распределение х человеко-индексов /=!,..., п по отношению к работо-индексам /=1,..., п, для которого сумма оценок d,, будет максимальной.

Задача распределения решалась методами обычного линейного программирования (см. работу Г. Данцига [51]) и с помощью специального алгоритма, подобного одному из описанных в работе Дж. Мункреса [61]. Данный метод является, по существу, специализацией алгоритма Хичкока для транспортной задачи (см. статью Л. Форда и Д. Фулкерсона [7i]).

Если перестановка х обладает свойством д;

"--Тп

для любой перестановки у, то мы говорим, что X минимизирует матрицу (d;.).

Если матрица (di.j) обладает тем свойств-о,м,. что X минимизирует матрицу (d.j) тогда и только тогда, когда минимизирует (dij, то мы говорим, что d « d эквивалентны. Ясно, что решить задачу распределения для некоторой ма-прицы - все равно что решить ее для всех эквивалентных матриц.

Теорема. Если дана некоторая вещественная матрица (di,i) размерности пХп и произвольные векторы (а) и (bi) порядка п, то матрица (rftj) с элементами i,j== =di,j-Gi + bj эквивалентна матрице 1(,3).

Доказательство. Если л: -перестановка целых 1,..., п, то числа bt,..., 6„ отличаются от чисел Ь,..., Ь.

только порядком расположения. Следовательно, "Ь

«=1 *

= 2 6г. Теперь предположим, что перестановка л; мини-

мизирует матрицу (dj, j), и пусть у - любая перестановка чисел Тогда имеем равенство

t=i г=1 t=i

«=i t=i

которое и показывает эквивалентность d и d.

Из этой теоремы следует, что, если мы найдем последовательность матриц, начинающуюся с матрицы (г,з) и кончающуюся матрицей (gj.j), каждая из которых получается из предыдущей вычитанием некоторого числа из всех элементов строки или столбца, со всеми aj.jO и если мы найдем перестановку х со всеми аг х=0,тох

минимизирует (dij). Это основа для алгоритма, цред-ставленного выше.

Анализируя ход алгоритма шаг за шагом, можно найти верхнюю границу числа шагов, необходимых для получения решения. Кроме .того, можно показать, что Верхняя граница действительно достигается для специальной матрицы с элементами dij- (i-1) Х(/-1).

Расчет времени. Алгоритм был закодирован автором для машины IBM 709 на нзыке SCAT (код язы-

ка SCAT вместе с отчетом будет рассылаться через SHARE). Результаты серии экспериментов составили основу для оценки продолжительности нахождения минимизирующей перестановки для данной матрицы. Эти эксперименты, результаты которых приведены на рис. 1, 2, 3, обсуждаются ниже.

Ни в одном случае начальный шаг (ом. алгоритм) преобразования матрицы в неот1рицательную матрицу,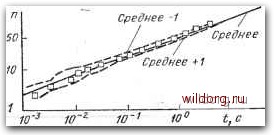

Рис. 1. Бремя, затрачиваемое алгоритмом «Распределение» для нахождения оптимального решения.

Матрицы - случайные; значения элементов - от О до 2"-1; □ - данные точки (каждая представляет средний результат для 50 случаев). Линия регрессии

t=U6rfi мкс.

50 -10 -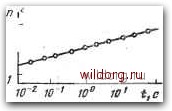

Рис. 2. Время, затрачиваемое алгоритмом «Распределение» для нахождения оптимального решения.

Матрицы - наихудшие; О - данные точки. Линия регрессии «94.7П* мкс.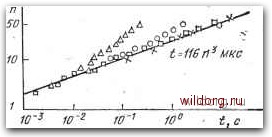

Рис. 3. Влияние ограничения последовательности значений матриц на время решения.

Матрицы - случайные; значения элементов - от О до 2*-1. Данные точки (каждая представляет средний результат для 20 случаев): Л соответствует ft=2: 0-ft=6; D-ft-IO; X-ft-23.