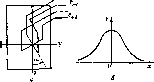Рис. 2.3. ный кодирующий элемент графики (а) и его ВМХ (б)

вием для применения вертикальных витков является угловая зависимость амплитуды снимаемых сигналов

- cos а,

где М - взаимная индуктивность съемного витка и шины возбуждения X, Y при угле между ними а = 0.

Очевидно, что в таком виде элемент неработоспособен. Решение задачи состоит в том, что вводится дополнительный съемный виток 3, расположенный ортогонально первому. Амплитуда сигнала на выходе дополнительного витка

е„2 = М - sin а.

Сигналы ортогональных витков преобразуем согласно формуле

""-(coscx + sincx) = £2 (2.1)

Поскольку результирующая амплитуда сигнала Е не зависит от а, то тем самым найден метод получения выходного сигнала, независимого от углового положения съемника. Если геометрические размеры рамок выбрать такими, чтобы они располагались в той части пространства на пересечении координатных проводников, где магнитное поле однородное, то амплитуда сигнала £ не зависит также от осевого наклона съемника координат.

Вольт-метрическая характеристика элемента, показанная на рис. 2.3, б, совпадает с зависимостью горизонтальной составляющей поля рассеивания несимметричной полосковой линии в перпендикулярном направлении при ее возбуждении импульсами тока с временем нарастания т.

Кодирующий элемент индуктивных устройств ввода непрерывной графической информации (НКЭГ) представляет собой многовитковую катушку и пересечение координатных шин, расположенных в параллельных плоскостях. Катушка вместе с визирными метками образует курсор, который вручную совмещается с точками изображения.

Для устранения погрешности кодирования за счет неточности совмещения меток курсора с центром съемной катушки предложено за-

Рис. 2.4. Микрополосковый кодирующий элемент графики

Рис. 2.5 К расчету выходного сигнала курсора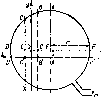

менить катушку печатным круговым проводником (рис. 2.4), который легко получается одновременно с визирными метками?методом фотохимического травления фольгированного диэлектрика. Вторая существенная составляющая погрешность, вызванная краевыми эффектами рабочего поля [34], устранена благодаря исключению взаимовлияния между координатными линиями при их выполнении в виде несимметричных полосковых линий.

Найдем вольт-метрическую характеристику курсора, представляющую собой зависимость выходного сигнала кругового витка от расстояния его центра до координатной шины:

Здесь неизвестной является зависимость взаимной индуктивности {х) кругового витка в виде несимметричной полосковой линии и одиночным проводником, проходящим параллельно линии на расстоянии л: от ее оси:

М{х) =

Мо для хс;

(2.2)

М ® для л;>с,

где Л1„ - погонная взаимная индуктивность; с - ширина зоны однородного магнитного поля; в - постоянная спада магнитного поля.

Учитывая, что участки кругового витка (рис. 2.5) ДА и АГ включены встречно по отношению к координатной линии, записываем

М {x) = 2 J {x) dx - 2lM {x) dx, (2.3)

где А, D, F - проекции соответствующих точек кругового витка на ось x.

Находим М (х), предполагая, что координатная линия расположена слева от центра кругового витка (см. рис. 2.5):

{x) = 2Мос {x) + 2Мав- (х) + 2МвА {х) \- 2Ma-f- [х). (2.4)

Запишем слагаемые формулы, пользуясь выражением (2.2). Выразим ординаты точек кругового витка с радиусом г через х:

МсВ(л:) = М„ j dy.

МвЛ (X) = М„ j

(2.5)

Учитывая, что все слагаемые формулы (2.4) имеют общий множитель iWo, представляем взаимную индуктивность в виде (л:) == Мо4ф (л:), где /эф - эффективная длина кругового витка, равная удвоенной сумме интегральны* функций.

Зависимость 1 получена путем численных расчетов на ЭВМ интегральных функций (2.5) при следующих значениях параметров: / = 5 мм, с = 0,2 мм, в = 0,3 мм (кривая/) и г = 5 мм. с = 0,5 мм, е = 0,6 мм (кривая 2). Результаты вычислений представлены па рие. 2.6. Рассчитанная зависимость с точностью до постоянного множителя соответствует вольт-метрической характеристике НКЭГ.

Крутизна начального участка S == Mljbx на интервале [0, -j практически не изменяется. Поэтому радиус кругового витка «виду линейности нужно выбирать равным удвоенному расстоянию между координатными линиями. Небольшое увеличение крутизны в конце рабочего интервала компенсируется уменьшением коэффициента усиления предварительного усилителя в области больших сигналов. Зависимость (2.5) позволяет заключить, что крутизна в большей мере зависит от коэффициента погонной взаимной индуктивности, чем от параметров сив, характеризующих локализацию магнитного поля линий.

Расчетная разрешающая способность устройства ввода непрерывной графической информации (см. рис. 2.6)

= Д, = -01. (2.6)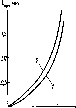

0 2 x,v\n

Рис. 2.6. Зависимость эффек-

А;с=

сГнияТо це7т;ГдГГр: При значениях параметров А. = 5 • 10- В. инатной шины х = 10~* с, = 0,05 А, М. = 0,5 • 10~®Гн

имеем Ал: = Ау = 5 мкм. Полученная величина значительно превышает аналогичную, достигнутую в лучших зарубежных образцах [37. 38].

2.3. Микрополосковые кодирующие элементы линейных н угловых координат

Рассмотренный в параграфе 1.3 дифференциальный считывающий элемент в виде встречно включенных параллельных участков полос-ковых линий имеет максимальную крутизну и поэтому используется для считывания пространственных кодов и построения дискретных КЭ. Однако такие элементы не могут быть организованы в виде матрицы с шагом по столбцам меньше, чем Я,/2. Указанное ограничение может быть снято, если применить КЭ, показанный на рис. 2.7.

Шина возбуждения / пересекает съемные шины 2 под углом, близким к 45°, что позволяет получить расстояние между линиями считывания двух соседних элементов, равное удвоенной ширине проводника, т. е. 0.3-0.4 мм при обычной технологии печатного монтажа. Как будет показано в параграфе 4.4, это свойство используется для согласования отсчетов в многошкальных преобразователях линейных и угловых перемещений. Движение модулирующего элемента 3 приводит к амплитудной модуляции выходных сигналов, которые трансформируются из шины / в шину 2.

Найдем вольт-метрическую характеристику и сравним основные параметры КЭЛ-2 с базовым. С достаточной для практики точностью амплитудная зависимость выходных сигналов такого элемента аппроксимируется выражением

e„(;c)-y„sin

- X,

(2.7)

где Vm - максимальная амплитуда выходного сигнала; Я, - период пространственной частоты модулирующего элемента.

Найдем максимальную амплитуду сигналов t/„. Согласно формуле (2.7) первый максимум наблюдается при х == Я,/4. т. е. при смещении середины модулирующей плоскости относительно линии считывания на Я,/4. В этом положении взаимная индуктивность участков шин /. 2 на верхнем пересечении равна ЬаМ (а), а на нижнем - М (а). Учитывая, что верхние пересечения индуцируют в съемной шине сигналы противоположной полярности, а ток возбуждения имеет экспоненциально нарастающий фронт т и амплитуду /„, получаем

= е„ (- ) = 2 [М (а) - б„М (а)] . Подставив значение U„ в формулу (2.7), найдем ВМХ

2Л1(а)(1-6„)/„ . 2я (X) =---sin - .

(2.8)

(2.9)

Крутизну ВМХ получим путем дифференцирования начального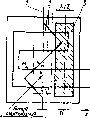

участка:

откуда крутизна преобразования

АШЩ-Ьи (2.11) Разрешающая способность имеет вид

Ах=-

Рис. 2.7. Кодирующий элемент линейных перемещений

Деи

5 4я/И(а)(1 б •

(2.12)

При значениях параметров Де = 5 х X 10- В, Л = 2 мм, т = 10- с, М (а) = = 0.26 . 10- Гн, ба = 0.45, = 1 А расчетное значение Ajc = 5,8 • 10" мм.

Для базового элемента Ajc = 5 х X 10" мм. Это позволяет заключить,

что по разрешающей способности рассматриваемые элементы практически равноценны. Однако базовый элемент отличается большим линейным участком ВМХ. Поэтому применение базового КЭ предпочтительно для построения нониусных шкал. В то же время элементы считывания пространственного кода могут строиться на основе как базового элемента, так и КЭ с пересечением линий под углом 45

Рассмотренные КЭ могут использоваться в датчиках линейных и угловых координат. В одном случае модулирующие элементы выполняются в виде линейно шкалы, а в другом - круговой или барабанной.

Амплитуда считанного сигнала с КЭ пропорциональна числу индуктивно связанных участков шин возбуждения и съема СЭ, на которые одновременно воздействует МЭ. В связи с этим линейный КЭ можно представить в виде, показанном на рис. 2.8. Элемент (рис. 2.8, б) обладает компактностью и может быть применен в прецизионных датчиках позиционирования, цифровом измерителе допусков, датчиках малых перемещений. Крутизна ВМХ такого элемента равна двойной крутизне базового КЭ,

В датчике позиционирования совмещение осей СЭ и МЭ соответствует отсутствию сигнала на выходе съемной шины, а значение амплитуды сигнала положительной или отрицательной полярности определяет отклонение оси МЭ от СЭ в ту или другую сторону. Аналого-цифровое преобразование амплитуды считанного сигнала указывает на цифровую величину отклонений осей. На этом основании можно строить цифровые измерители линейных и угловых допусков. Но 1Юскольку амплитуда считанных сигналов КЭ зависит от высоты МЭ над СЭ, то такие измерители допусков должны иметь первичный эталон, т. е. контрольные КЭ, по которым оценивается и регулируется показание АЦП,

"1

Рис. 2.8. Считывающие элементы с повышенным уровнем с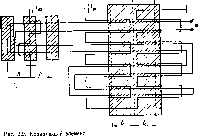

датчика допусков с контролем эталона

КЭ измерителя допусков, показанный на рис. 2.9, содержит основной и дополнительный СЭ, информационный и три контрольных МЭ, причем информационный МЭ связан с основным СЭ, а контрольные МЭ - с дополнительным СЭ. Шаг между контрольными МЭ равен первичному эталону, а расстояние между осями основного и дополнительного СЭ равно расстоянию между осями информационного и среднего контрольного МЭ.

Если ось информационного МЭ совпадает с осью основного L, оси среднего контрольного МЭ и дополнительного СЭ также совпадают, и сигналы при возбуждении СЭ равны нулю. Если ось левого контрольного МЭ совпадает с осью дополнительного СЭ, то при возбуждении этого СЭ сигнал на выходе съемной шины равен нулю, а