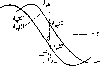Рис. 1.29. Зависимость амплитуды отсчетов корреляционных функций от времени при наличии фазового сдвига

каждой последовательности исполь-зуется только одна из опорных последовательностей h, (iTi) или he (iTi). Напряжения отсчетов корреляционных функций процессоров А, (О и Ащ {t) показаны на рис 1 29 На интервале времени ЛГф = Аф/<й„ амплитудные зависимости отсчетов при малых Аф можно считать линейными.

Важным свойством зависимостей Лф, it) и Лф. (О от времени поступления отраженного сигнала является изменение полярности на интервале времени АГф. Это позволяет применить следующий алгоритм для точного вычисления временного положения А/,, отраженного сигнала относительно опорного. В момент / = О нужно измерить напряжения Лф, (0) и Л<р, (0) и выполнить вычисления по формуле

<= Л,. (0)4-Л,. (0) = <о„Иф.(0)+»ф,(0)1 • Вычисление значений Аф представляет собой растяжку временной шкалы на интервале АГф в масштабе Q = ф » где Лф (0)m,n- шаг квантования напряжения Лф (0) Положение временного интервала ДГфНа временной шкале < при необходимости можно найти пороговым методом. В устройствах пространственного зрения в этом нет необходимости, поскольку глубина пространственной сцены AD = -= сАГф/2. Для гармонического модулируемого сигнала разрешающая способность по дальности

AD =

с (Фг - Ф1)

В устройствах пространственного зрения при формировании псевдошумовых последовательностей целесообразно использовать инфракрасные светодиоды или полупроводниковые лазеры в режиме импульсной модуляции. В качестве задающих выгодно применять цифровые схемы. Элементами псевдошумовой последовательности являются положительные или отрицательные перепады интенсивности излучения, а на выходе корреляционного приемника - положительные или отрицательные перепады напряжения. В этом случае измеряемый интервал времени АГф = tф/2, где - длительность линейного нарастания и спада интенсивности излучения, а разрешающая способность AD = ctlQ- Отсюда следует, что приемлемое для систем технического зрения разрешение AD = 1 мм можно получить при Q = = 256 и <ф = 3,3 НС. Приняв длительность элемента псевдослучайной последовательности = At = 12 не при N = 1024, получим время обработки одной точки пространства равным 12 мкс, а пространство, содержащее 256 X 256 точек, будет закодировано за 0,9 с.

приемников импульсных последовательностей со слу-

чайной полярностью в качестве зондирующих сигналов практически исключает возможность расшифровки их структуры за время смены последовательности по заданной программе, так как не существует другого способа ее приема кроме корреляционной обработки. Особенность этого способа заключается в исключении операции усиления сигнала, уровень которого может не превышать уровня помех. Причем эсхрективная корреляционная обработка предполагает наличие большого объема априорной информации, заложенной в опорном сигнале.

Предпосылкой для распространения твердогельной микроэлектроники на область корреляционных приемников высокочастотных сигналов является применение функциональных элементов для вычисления коэффициентов корреляционной функции с эквивалентной производительностью не менее 10" операций умножения отсчетов сигнала на коэффициент с суммированием результата.

функциональные элементы корреляционных приемников высокочастотных сигналов - фронтальные процессоры - можно построить на основе транзисторных перемножителей в режиме суммирования заряда.

Фронтальные процессоры пригодны для построения приемников сложных сигналов, применение которых способствуег улучшению пространственно-временного разрешения и помехоустойчивости. Нх целесообразно применять в сочетании с цифровыми сигнальными процессорами, выполняющими вторичную обработку отсчетов корреляционных функций и программирование сложных сигналов,

Глав

СИСТЕМА КОДИРУЮЩИХ ЭЛЕМЕНТОВ ДЛЯ ПЕРИФЕРИЙНЫХ ИЗМЕРИТЕЛЬНЫХ УСТРОЙСТВ НА ОСНОВЕ МИКРОПОЛОСКОВЫХ ТРАНСФОРМАТОРОВ

я к кодирующим элементам

Сферу передачи информации в кибернетических системах делят в основном на два вида сигналов: электрические и механические. Информационным параметром электрических сигналов чаще всего служит напряжение, а механических - перемещение. Благодаря большой скорости распространения электромагнитных колебаний и высокому уровню развития электроники электрические сигналы занимают господствующее положение в системах дистанционной передачи и переработки информации Механические сигналы являются естественным носителем информации о важнейших физических параметрах (перемещении, скорости, ускорении, силе, давлении, расходе вещества, температуре), а также используются для передачи символьной и графической информации от человека к системе переработки [16, 17]. Поэтому механические сигналы являются основными в системах получения первичной информации.

Преобразование непрерывных и дискрегных механических сигналов в амплитудно-модулированные импульсные электрические сигналы выполняют КЭ. Для механических сигналов характерно §олее широкое распространение двухмерных величин, чем для электрических. Такие свойства механических сигналов, как дискретность, двух-мерность, непрерывность, предъявляют различчые требования к вольт-метрическим характеристикам, что порождает многообразие типов КЭ.

ВМХ выражается произведением входных сигналов. В этом смысле КЭ являются модуляторами [18]. Различие между ними состоит в том, что модуляторы осуществляют перемножение электрических сигналов, один из которых является информационным, а другой - переносчиком, в качестве которого используется обычно гармонический сигнал, выбираемый из условия дистанционной передачи. В КЭ инфоомациои-ным сигналом служит перемещение, а модулируемый электрический сигнал и модулируемой параметр выбираются из условий точности и надежности цифрового преобразования.

Конструктивно и функционально КЭ делится на МЭ и СЭ. К МЭ прикладывается входной информационный сигнал, а к считывающему-сигнал возбуждения. Съем информации производится либо с модулирующего элемента, либо со считывающего. Информационное воздействие на КЭ вызывает перемещение МЭ относительно считывающего, благодаря чему изменяется значение модулируемого параме!-ра выходного сигнала.

Один МЭ может обслуживать множество считывающих, объединенных, как правило, в матрицу. Если каждый СЭ матрицы снабжен отдельным МЭ, то матрица КЭ в режиме кодирования двоичной информации функционально оказывается идентичной матрице ЗЭ программируемых вручную постоянных запоминающих устройств [19, 20]. Однако КЭ в отличие от запоминающих предназначены не для хранения, а для преобразования информации.

Рассмотрим требования к полосе пропускания КЭ в режиме преобразования непрерывной информации. Устройства цифрового кодирования выполняют функцию импульсно-кодовон .модуляции. Им-пульсно-кодовое представление непрерывных сигналов повышает помехоустойчивость информации в системе переработки и исключает зависимость точности преобразования от элементной точности схем [21].

Полоса пропускания задается полосой частот информационного и модулируемого сигналов с учетом операции перемножения, выполняемой КЭ. В этом смысле информационный сигнал S (/) характеризуется высшей гармоникой в спектре частот F,. В преобразователе применяются три вида модулируемых сигналов: постоянное напряжение Е, импульсные сигналы с минимальной частотой следования f „ = = 2F,, либо с произвольной F, = nF,,, где л„ > 1. Частотные свойства импульсных сигналов учитываются коэффициентом формы у.

Рассмотрим соотвегствующие модулируемым сигналам три схемы преобразования. Если модулируемым сигналом служит постоянное напряжение, то требуемая полоса пропускания КЭ минимальна и равна F„. Амплитудно-модулированное входным сигналом напряжение на выходе КЭ подвергается аналого-цифровому преобразованию с частотой отсчетов Fo = 2вч, которая определяется теоремой Котел ьнккова. По второй схеме дискретизация по времени с частотой

производится КЭ, на который поступают модулируемые импульсные сигналы с частотой F. Требуемая полоса пропускания КЭ лежит в 1штервале частот 2fвч - 2f„у. В третьей схеме преобразования частота модулируемых импульсов принимается равной л„Гвч, а потоса пропускания КЭ занимает 1Юлосу частот от до nF„r,y.

Оценку схемы преобразования проведем по максимальной чувствительности Ае при различении двоичных сигналов. Предположим, что для надежного рзличени я на входе решающего элемента требуется пикфактор Z=Ae/2U, где i/„- среднее квадратическое значение напряжения шумов, которое связано с полосой пропускания формулой Найквиста. Для первой схемы выполняется соотношение Ае? = = 2M6r/?f„>ln„ где - шум-фактор транзисторов входного каскада усилителя сигналов.

Соответствующие соотношения для второй и третьей схем имеют вид

А4 = Z32kTRF,,(Y-l)Авг. а4 = Z32kTRf„(у- 1)л„Л.

Отсюда следует, что наихудшую чувствительность имеет третья схема, а наилучшую - первая Однако такой вывод справедлив по отношению к «белому» шуму, спектральная плотность которого не зависит от час-

тоты 122, 23], а также без учета оптимизирующих свойств приемника сигналов [24]. Первая схема имеет принципиальный недостаток, состоящий в том, что она подвержена тепловому дрейфу нуля, так как предполагает применение усилителя постоянного тока. Недостаток первой и второй схем состоит в том, что они используют низкие частоты для передачи сигнала, где шум-фактор транзисторов значительно выше, чем на средних и высоких частотах [25].

Указанные недостатки несвойственны третьей схеме Для увеличения чувствительности воспользуемся той ее особенностью, что высокая частота модулируемых импульсов F, = пРач позволяет более эффективно применять импульсные фильтры, которые способствуют улучшению отношения сигнал/помеха на выходе во столько раз, во сколько период отсчетов 1/2/=",, больше периода высокочастотного модулируемого сигнала Fn [26]. Действие импульсного фильтра учитывается соотношением

из которого, учитывая формулу Найквиста, получаем Де» = Z32kTRFBr, {у-\) А.

Таким образом, по чувствительности третья схема при наличии фильтра равноценна второй, если шум-фактор в полосе частот от 2f„ до n„F„y считать постоянным. С учетом увеличения шум-фактора транзисторов на низких частотах предпочтение, однако, следует отдать третьей схеме. Кроме того, высокочастотная импульсная модуляция позволяет получить приемлемый коэффициент передачи по напряжению микрополосковых трансформаторов, что является необходимым условием их использования в качестве единой элементной базы для всего многообразия устройств преобразования механических сигналов. Поэтому эффжтивным методом улучшения КЭ следует считать расширение их полосы пропускания, благодаря которому спектр кодируемого сигнала переносится в область низких частот.

В связи с влиянием КЭ на надежность различения сигналов рассмотрим другие аспекты этой проблемы. Увеличение надежности различения, измеряемое вероятностью ошибок, достигается вследствие применения фильтров, т. е. улучшения приемника, а также увеличения различимости выходных сигналов КЭ.

Помехоустойчивость с помощью фильтров можно повысить за счет увеличения отношения сигнал/помеха в приемной части устройства перед схемой различения сигналов. С этой целью применяют квазиоптимальные (полосовые) и оптимальные линейные фильтры [27]. Их действие заключается в увеличении амплитуды сигнала в момент стробирования и подавлении помех вследствие усреднения амплитудных значений. Линейные фильтры эффективны при условии, что длительность входного сигнала существенно больше интервала корреляции случайной помехи. Если эго условие не выполняется, то в случае широкополосных КЭ с высокочастотной импульсной модуляцией т е-ется дополнительная возможность воспользоваться дискретными им-

пульсными фильтрами [28], расположенными после схемы-различения сигналов. Они позволяют получить требуемую вероятность ошибок при малых значениях пикфактора на выходе линейной части приемника и, таким образом, создают эффект увеличения отношения сигнал/помеха.

Надежность различения двоичных сигналов можно существенно повысить за счет увеличения различимости сигналов «О» и «1» на выходе КЭ. Теоретически вопрос о максимальной различимости сигналов решается на основе геометрической модели сигналов как векторов [22] в многомерном пространстве, которая впервые была применена К. Шенноном для доказательства пропускной способности канала связи [29]. В качестве координат многомерного пространства сигналов служат ортогональные функции, на которые раскладывается сигнал, например гармонические, функции отсчетов Котельникова и др В этом случае максимальная различимость интерпретируется как максимальное расстояние между векторами. В системе двух сигналов U„ (t) и L/j (t) расстояние

Оно максимально в случае противоположных сигналов U„ (t) = = - t/j (О- Поэтому выполнение требования представления «О» и «1» разнополярными сигналами одинаковой формы будем считать обязательным для КЭ, поскольку при данном условии преобразователи двоичных сигналов имеют наибольшую помехоустойчивость, что следует также из статистической теории потенциальной помехоустойчивости Котельникова для случая различения сигналов с минимальной вероятностью ошибок по «О» и «1» [30-32].

2.2. Микрополосковые кодирующие элементы УЦК двухмерных координат

Разработка специализированных устройств кодирования двухмерной дискретной координатной информации вызвана необходимостью автоматизации проектирования и производства микроэлектронной техники. Для этой отрасли характерны дискретность технологических операций, высокий уровень стандартизации размеров и автоматизации технологических "процессов Это обусловило преобладание дискретной входной и выходной графической информации. Такая информация задается матрицей двоичных элементов. При вводе каждому биту входной информации ставится в соответствие отдельный кодирующий элемент на плоскости планшета, на котором располагается кодируемое изображение. Особенность ввода дискретной информации состоит в повышенных требованиях к надежности: вероятность ошибок 10~-10. С целью уменьшения ошибок при вводе области чувствительности отдельных элементов не должны перекрываться. Если учесть, что необходимые значения шага дискретизации по координатам х и у составляют Д;с = Дг/ = 1,25; 2,5; 5 мм [33], то в качестве основной технической задачей при разработке дискретных элементов для кодирования графики (ДКЭГ) следует признать достижение тре-