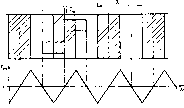Рис. 4.3. ВМХ базового чувствительного элемента

Продифференцировав выражение (4.9), найдем максимальную амплитуду прн X = 0:

(4.11)

Таким образом, более точное значение амплитуды ниже, чем определен-иое по кусочно-линейной ВЛ\Х элемента. Метрологические свойства отдельного кодирующего элемента на интервале к/2 невысоки, поскольку амплитуда считанных сигналов согласно (4.11) зависит от многих электрических параметров (амплитуды и фронта импульса тока, коэффициента усиления в мультиплексоре) и конструктивных (расстояния между модулирующим элементом и чувствительным, геометрических размеров модулирующего элемента). Поэтому по абсолютному атачению амплитуды считанного сигнала перемещение модулирующего Э1емента относительно считывающего можно найти с невысокой точно-вгью.

Метод повышения точности кодирования перемещения по амплитуде сигнала основан на двух факторах. Первый состоит в том, чо для оп-рэделгния перемещения используется только начальный участок ВМХ, а второй - в применении интерполяции по ВМХ двух считывающих элементов, смещенных на небольшое расстояние по сравнению с X.

Использование только начального участка ВМХ достигается применением матрицы pS ЧЭ, в которой считывающие элементы сдвинуты по нониусу относительно модулирующих, вследствие чего ось х ока-зызается квантованной с шагом At, = X/pS. Благодаря тому что ВМХ КЭ описывается нечетной функцией от расстояния между серединой мстулирующего элемента и линией считывания, любому положению модул нруюш.его элемента на оси х соответствуют два КЭ, последовательный опрос которых дает разнополярные сигналы и в. На рис. 4.4 показаны ВМХ таких КЭ. Ось считывания первого КЭ занимает положение X = О, а второго - X = Ах». Середина модулирующего элемента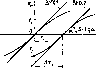

находт1тся в точке х = х. Поскольку начальный участок ВМХ/ линейный, то

x,ejS, (4.12)

где S - крутизна.

Однако в процессе эксплуатации УЦК трудно рассчитывать на постоянство крутизны S. Поэтому для практики имеет большое значение способ исключения влияния S на точность кодирования. Идея способа заключается в том, чтобы при каждом измерении измерять также S путем считывания сигнала со второго КЭ, который имеет ВМХ с одинаковой крутизной. Согласно рис. 4.4

e, = (Ax3-Xi)S. (4.13)

Подставив в (4.12) значение S, найденное из формулы (4.13), получим интерполяционную формулу

(4.14)

Рис. 4.4. Погрешность иитерполяцнои-иого метода определения координаты

В которой отсутствует крутизна.

Найдем погрешности определения х по интерполяционной формуле (4.14) в случае нелинейной ВМХ и при неравенстве крутизны пары считывающих элементов. Предположим, что ВМХ имеет вид (4.9). На интервале Ах, = K/pS амплитуда сигнала "

.. = </.3lnJi(l+).

Интерполяционная формула дает приближенное значение

2л ху sin ----

(4.15)

(4.16)

По сравнению с линейной ВМХ имеет место абсолютная ошибка

6b = -Ki -xtnp = Ал

sin-Lv \

т-"Ч-- (-iT)

sin-Y + sin -- (I- Y) /

где V = ATi/AXg; = pS.

Относительную ошибку определим как е =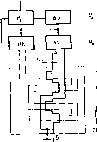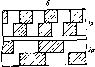

Рис. 4 5. Одиошкальный да1чик координат считывания пространственного

рис. 4.6. Трехотсчетиый цифровой датчик координат

Благодаря исключительной простоте изготовления кодовой шкалы наряду с большими допусками на взаимное расположение считывающих элементов и кодовых дорожек описанный ЦДК пригоден для построения измерителей длины в несколько десятков метров.

Остановимся на устройстве ленточного цифрового измерителя (циф ровой рулетки). В качестве пространственной кодовой шкалы в нем используется стальная лента с перфорацией, показанной на рис. 4.7.

Прямоугольные отверстия в мерной ленте имеют ширину Х,/2, шар "к и высоту, превышающую с запасом длину считывающего элемента в направлении линии считывания. На выходе импульсного компаратора

Ijinjinr

эпюра напряжения имеет пространственный период . Для повышения вдвое числа уровней квантования двоичный счетчик на выходе компаратора работает в режиме счета перепадов входного напряжения. Так как данное устройство работает на принципе счета импульсов, то перед каждым измерением требуется устанавливать счетчик импульсов в «О».

Остановимся на одной важной особенности цифровых измерителей длины со шкалой на ос1юве полосковых модуляторов. Она следует из того факта, что разрешающая способность считывания положения модулирующего элемента Ал; <g X даже при отсутствии импульсного фильтра. Поэтому описанные выше устройства представляют собой дискретные измерители длины с шагом %f1 и случайной погрешностью, которая на несколько порядков меньше "к. Это свойство можно использовать для повышения точности измерения длины или угла.

Если предложенный метод записи позиционных кодов методом формирования проводящих и изоляционных участков по технологии фотохимического травления, допускающий статическое считывание и высокую точность расположения кодов, решает проблему получения высокотехнологичных мерных шкал практически любой длины, то для определения высокой разрешающей способности нужен другой метод, основанный на той же элементной базе, так как требование ее единства является превалирующим.

На первый взгляд может показаться, что шкалу точного отсчета, способную разделить минимальный период шкалы грубого отсчета ?о на требуемое число уровней квантования, легко получить, пользуясо ВМХ базового считывающего элемента. С этой целью достаточно в шкалу ГО ввести дополнительный разряд с модуляторами, показанными на рис. 4.7. Считывание с такой шкалы дает пилообразную характеристику (см. рис. 4.2) с периодом X,. Так как амплитуда напряжения зависит линейно от перемещения, то дополнительный разряд можно использовать для измерительного преобразования

где Era - целое число уровней квантования напряжения осуществляемое с помощью АЦП. Зная 5 = j, получаем х = nSAx.

Указанный амплитудный метод аналогового преобразования широко применяется в технике, так как он позволяет измерять неэлектрические величины через измерение напряжения [92]. Однако два принципиальных недостатка не позволяют его рекомендовать для кодирования линейных перемещений. Первый основан на необходилюстн

Таблица 4.1. Матрица выходных состояний СЭ

Поскольку аргументы функции принимают дискретные значения, а сама функция имеет только два значения («1» и «О»), то ее удобно представлять матрицей выходных состояний (табл. 4.1).

Рассмотрим способы заполнения таблицы. Способ сигналограмм основан на использовании известных ВМХ формирователей сигналограмм (см. рис. 4.3). Он позволяет получить столбец табл. 4.1 при перемещении модулирующего элемента выбранного типа на интервале перемещения Я„. При заполнении строк целесообразно воспользоваться схемами шкал, показанных на рис. 4.8 и отображающих взаимное расположение модулирующих и считывающих элементов. С этой целью в схему нужно ввести номера считывающих элементов и помимо оси проводящей полоски обозначить ось щели между полосками (двойные линии на рис. 4,8). Полученная этим методом матрица /? = 3, s = 4 представлена в табл. 4.2.

Вполне очевиден экспериментальный способ получения матрицы выходных сигналов, который также используется для проверки правильности функционирования ЦДК. Oi? заключается в задании шагов перемещения Кз и последовательном переборе адресов СЭ, например в циклическом режиме. Этот режим используется также для автоматической регистрации номера /Сэ- Первый этап реализуется функциональной схемой устройства (рис. 4.9) в следующей последовательности. Блок управления Б У отключает ЦАП, устанавливая на входах ИК нулевые уровни. Коммутатор тока и мультиплексор переводятся в режим последовательного опроса КЭ сериями импульсов, количество которых задается импульсным фильтром в зависимости от требуемой величины АХ. На выходе фильтра для каждого интервала Ks будем получать сигналы соответствующей строки табл. 4.2. Рис. 4.9. Функциональная схема матрич- Двоичный код номера интервала иого цифрового датчика координат К считывается со счетчика пере-

I 4.2. Матрица значений сигналов СЭ

бора адресов в момент переключения выходного триггера фильтра из «Ь в «О». Этот код передается в старший разряд выходного регистра устройства. Если. ограничиться определением номера считывающего элемента, то разрешающая способность устройства Ах = Kjps невелика, так как построение матрицы большого размера ведет к увеличению габаритов и аппаратурных затрат.

Учитывая геометрические размеры преобразователей перемещений с фотоэлектрическим считыванием фирмы «Heidenhain» (ФРГ) 193], принимаем матрицу чувствительных элементов 5x4, которая позволяет получить АлГд = 0,1 мм при Я„ = 2 мм.

Дальнейшее значительное повышение разрешающей способности легко получить, если воспользоваться начальным участком зависимости амплитуды считанных сигналов от перемещения в пределах Jps. В этой области ВМХ линейна, так как не сказываются краевые Эффекты КЭ и нелинейность динамической характеристики усилителя сигналов. Предположим, что ось матрицы совпадает с точкой А,