Описанную выше физическую картину взаимодействия узкого токонесущего проводника и широкого съемного подтверждает эффект увеличения взаимной индуктивности при относительном смещении этих проводников. На рис. 2.24, б показана зависимость от расстояния между осями проводников в направлении оси х. Кривая / соответствует линиям cbi = 0,2 мм, dl = 0,2 мм; = 0,6 мм, d = 0,195. Максимум кривой приходится на расстояние, равное примерно половине ширины линии 2.

Э4х})ект увеличения потокосцепления при смещении зонда большой ширины ошибочно можно истолковать как увеличение напряженности поля на краю линии / 1321. Избежать подобных ошибок измерения поля помогает использование высокочувствительной аппаратуры, позволяющей применять одновитковые миниатюрные зонды.

Проведенные исследования позволяют сформулировать следующие требования к зонду или к съемной линии КЭ. Ширина измерительного проводника зонда должна быть такой, чтобы магнитное поле исследуемой линии в перпендикулярном к ней направлении изменялось незначительно на расстоянии, равном ширине зонда.

Практически для несимметричных линий с = di = 0,2 мм удовлетворительная точность измерений обеспечивается зондами с шириной проводника 0,1-0,2 мм (зависимость 2).

Оценим влияние эффекта самоэкранирования на величину коэффициента передачи ИПТ по напр " ИПТ с /i = /а = /о

). Падение напряжения на входе

или его амплитуда

Ui(t) = Lo-

О)гласно (2.22) выходное напряжение

t/2m=Mo.21-.

Коэффициент передачи по напряжению

По номограмме рис. 2.17 для исследуемой линии Lg = 0,47 нГн/мм. При съемной линии (2=0,1 мм) согласно рис. 2.25 Мол =0,36 нГн/мм мКи = 0,76, а при = 0,6 мм М0.21 = 0,21 нГн/мм, Ки = 0,45. Поэтому эффект самоэкранирования существенно влияет на коэффициент передачи по напряжению.

2,8. Расчет взаимной индуктивности линий,

пересекающихся под углом

Распространенным элементом ИПТ является пересечение участков первичной и вторичной цепей под некоторым углом, благодаря которому появляется возможность уменьшать расстояния между линиями

считывания КЭ, увеличивать допуск на горизонтальное смещение вторичной цепи относительно первичной [401.

Примем следующий способ аппроксимации зависимости на рис. 2.23:

(Mf, при хс, Мое-/« при х>с, где с - абсцисса точки пересечения прямой Мо и касательной, проведенной к точке перегиба А экспериментально полученной кривой Мо (х); 0- расстояние от точки с до точки пересечения касательной с осью X.

Пусть линия неограниченной длины / (рис. 2.25) делит линию 2 длиной /а, которая пересекается с линией / под углом а, на отрезки k и /г, В свою очередь, участок й делится на отрезок С, расположенный в равномерном поле линии /, и на отрезок где поле убывает по экспоненте. На участке равномерного поля взаимная индуктивность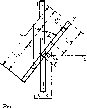

2.25. К расчету взаимной индуктивности линий, пересекающихся под углом

МоС cos а = Mffi ctg а.

(2.38)

Для определения взаимной индуктивности участка С с линией 2 выделим на этом участке на расстоянии х элемент dl бесконечно малой длины. На длине этого участка поле можно предположить равномерным, тогда по аналогии с (2.38) запишем

dM(x) = Moe ctgctdx.

(2.39)

Взаимную индуктивность по всей длине отрезка С найдем интегрированием выражения (2.39) вдоль проекции этого отрезка на ось х: •

Л1(х)= J Modgae erfx.

(2.40)

Произведем замену С sin а = /г sin а - с и после интегрирования получим

М (х) = Alectga (1 (2.41)

В силу осевой симметрии магнитного поля аналогичные выражения выполняются и для участка линии 2. Для пересечения линий окончательно запишем

(х) = 2сМо ctg а + Мов ctg а (1 - Г"®""""""») -f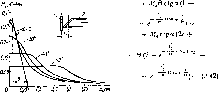

Используя приведенные выше рассуждения, легко найти взаимную индуктивность отрезка линии 2, который находится за пределами зоны равномерного поля линии / и задается проекциями концов Xi и на ось х:

Рис. 2.26. Зависимость взаимной индуктивности линий, пересекающихся под углом, от расстояния между ними

Ма(л:) = MpCtga Je dx.

где а = arccos .

Выполнив интегрирование, получим

Л1а(л:) = Мовс1

(2.43)

Для проверки расчетной формулы (2.42) для линии / с параметрами = 0,2 мм, = 0,2 мм и линии 2 с da = 0,195 мм, = 0,2 мм длиной /г = 125/cosa мм экспериментально получена зависимость Ма (дг) от расстояния середины отрезка до оси линии / при различных значениях а (рис. 2.26). Для кривой а == 0° получены значения с = 0,06 мм и е = 0,25 мм. Относительное отклонение расчетных данных от экспериментальных во всем диапазоне а и х не превышает ±15 %, что можно считать весьма удовлетворительным при расчете устройств дискретной техники.

Кривые зависимости (х) свидетельствуют о том, что увеличение угла пересечения между полосковыми линиями ведет к увеличению расстояния вдоль оси х между осью линии / и центром линии 2, в пределах которого взаимная индуктивность линий не изменяется. Это свойство пересекающихся под углом линий широко используется при конструировании матриц кодирующих элементов для расширения допусков на смещение в горизонтальной плоскости между шинами возбуждения и съема сигналов.

2.9. Им

е трансфо

с управляемым коэффициентом передачи

Основной характеристикой ИПТ является коэффициент передачи напряжение на выходе - ток на входе, полученный из равенства (2.22):

Как было показано выше, на принципе изменения i

гекта

передачи строятся все КЭ. Наиболее легко осуществимым и технически приемлемым способом управления является наложение на ИПТ проводящих поверхностей или короткозамкнутых витков, действие которых состоит в изменении величины Мх. Практическое использование управляемых ИПТ в настоящее время сдерншвается отсутствием теории расчета их конструкции.

Основной нерешенной задачей является определение величины растекания токов в наложенной проводящей поверхности и оптимальных размеров короткозамкнутого витка.

Сформулируем задачу о короткозамкнутом витке. Полосковая линия / (рис. 2.27) образует трансформатор совместно с полосковой линией 2. Поверх линии / накладьшается короткозамкнутый виток 3. Действие короткозамкнутого витка состоит в том, что магнитное поле тока индуцирует в нем ток ig, который вызывает на выходе шины 2 напряжение Viy. меньшей амплитуды по сравнению с его значением при отсутствии шины 3 и. Значение этого уменьшения зависит от расстояния между элементами витка 3, по которым протекают токи tg и tl. Оно представляет собой коэффициент модуляции б = VJV-

Увеличение ведет к росту индуктивности и, следовательно, снижению TiKa /з и увеличению /гк, а уменьшение г« вызывает увеличение потокосцепления шины 2 и удаленного участка шины 5, изменение тока 1з в котором приводит также к увеличению напряжения Угк. Таким образом, существует оптимальное значение Гк. при котором С/гк минимально. Очевидно, что минимуму t/gK соответствует минимум магнитной энергии в системе в момент протекания тока i.

Найдем зависимость (/гк от параметров линий /, 2 (рис. 2.27, а). Предположим, что между полосковыми линиями существует взаимодействие магнитных потоков, заданных коэффициентами взаимной индукции, как показано на рис. 2.27, б. Запишем уравнение Кирхгофа для контура 2:

М,, + 4--Мз, 4- = 4- + t/2K. (2.44)

Контур 2 работает в режиме холостого хода, что позволяет исключить первый член в правой части уравнения (2.44). Уравнение Кирхгофа для контура 3 имеет вид

(2.45)

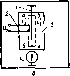a модуляции выходного напряже-

Для упрощения положим, что = м; мзз = miy= М23 Уравнение (2.45) упростится:

откуда

После подстановки в (2.44) получим

ls - 2Л1з

(2 46)

(2 47)

Согласно ранее принятой аппроксимации мз = Лхгб ** .

Принимая во внимание, что коэффициенты взаимной индукции и самоиндукции выражены в нГн/мм (представлены погонными величинами), индуктивность замкнутого контура также представим теми же величинами l, lg = 2lo (/« + Гк) или в относительных единицах:

= 2LA(1 +гок), где гок = rjb; - погонная индуктивность линии 3.

Так как - !„ (1 - е~~), то при i = О

Подставляя полученные величины в (2.47) и вводя обозначения Л = mjm12 и S = 1о/Л21. записываем

(2.48)

Поскольку мц- = и г, то коэффициент модуляции выходного напряжения короткозамкнутым витком

2[В(Ц-л.«)-Г I

(2.49)

Численное исследование выражения (2.49) позволяет установить, что минимум б выполняется при = 30 для линий с dl - 0,2 мм и bi = 0,2 мм. При расстояниях между линиями 1,2из, равных 5 мкм, минимальное значение б = 0,84.

Рассмотрим случай, когда на ИПТ, состоящий из линий / и 2, наложена проводящая поверхность 5 (рис. 2.27, в). Найдем б для этого случая, предполагая, что ток Фуко проходит по двум контурам оабо и овго. Если предположить, что индуктивность двух параллельных участков аб и вг мала по сравнению с участком 00, то индуктивность для тока Фуко одного из контуров Lg = lb, и формула (2.49) примет вид

(2.50)

Коэффициент ослабления сигнала для двойного контура с погонной индуктивностью Lo = 0,42нГн/мм приг = 6 составляет б = 0,35.

В этом случае увеличение ослабления достигнуто за счет уменьшения со-ивления контура вихревому току, наименьшего сопротивления

м,нГн/т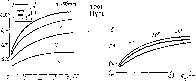

0,1 0,2

Рис. 2.28. Зависимость взаимной индуктивности ИПТ от расстояния до модулирующего элемента

Рнс. 2.29. Зависимость коэффициента модуляции от расстояния между модулятором и шиной возбуждения