ИПТ работает в режиме дифференцирующего трансформатора с малой постоянной времени.

Использование полосковых трансформаторов для построения КЭ основано на их способности изменять полярность трансформируемо-

го импульса в зависимости от величины угла пересечени;

шин 7 и 2.

При одинаковом направлении тока в шине / трансформаторы (см. рис. 2.14, а, б, г) в шине 2 обеспечивают импульсы тока противоположной полярности. Второе важное свойство таких полосковых систем, эффективно используемых для модуляции амплитуды импульсных сигналов, заключается в возможности изменять коэффициент трансформации при наложении бесконтактным способом на пересечение шин 1, 2 проводящей поверхности или короткозамкнутого витка. Влияние проводящей поверхности заключается в уменьшении потокосцепления между первичной и вторичной шинами вследствие возникновения в проводящей поверхности вихревых токов (токов Фуко).

На современном уровне исследования переходных процессов в системах несимметричных полосковых линий достоверные параметры для их расчета можно получить только экспериментально. В настоящее время существуют методы расчета полосковых линий при следующих упрощениях: монохроматическое поле [41], малая высота линии по сравнению с шириной, «толстое» основание 5 (см. рис. 2.14, г) [42, 43]. Для ИПТ указанные упрощающие обстоятельства не имеют места. Прежде всего при питании трасформатора импульсным током представляет интерес магнитное поле не установившегося процесса, как при гармоническом воздействии, а поле переходного процесса в момент включения и выключения непериодического импульса тока (2.17). Как известно, одиночный импульс выражается непрерывным спектром гармонических составляющих (спектральной плотностыо). Непериодический Импульс можно считать периодическим с достаточно большим периодом следования и применить дискретное преобразование Фурье, но такой путь предполагает использование вычислительных мощностей для расчета ИПТ.

В устройствах кодирования дискретной графической информации наблюдается устойчивая тенденция к уменьшению шага квантования, а следовательно, и шага координатных шин, что вынуждает применять полосковые линии с минимальной шириной. Характеристики кодирующих элементов ПИУ других типов также улучшаются при уменьшении ширины токонесущего проводника полосковых линий. Поэтому предположение малой высоты линий по сравнению с шириной практически невыполнимо.

Предположение о «толстом» основании полосковых линий обычно делается Для упрощения граничных условий при составлении дифференциальных уравнений в частных производных [44, 45]. Однако в отношении ИПТ на базе многослойного печатного монтажа это упрощение неприемлемо в силу того, что толщина меди фольгированных диэлектриков d = 30 35 мкм. Она является «тонкой» для нижней граничной частоты спектра импульса магнитного поля и «толстой»-для верхней частоты.

Для подтверждения этого рассчитаем глубину проникновения плоской монохроматической волны с частотой 10» и 5 • 10 Гц Эти частоты близки к /„ - нижней граничной частоте и - высшей граничной частоте в спектре импульса магнитного поля, создаваемого током (2.17) длительностью 40 не с фронтом 7 не. Глубина проникновения плоской монохроматической волны

(2.18)

где ш - угловая частота; ц„ - магнитная проницаемость; а„ - удельная проводимость меди.

Из формулы (2.18) вытекает, что для = 10« Гц Д = 66 мкм, для /в = 5 . 10 Гц Д = 1 мкм, т. е. глубина проникновения на низких частотах Д > d, а на высоких Д < cf.

В формировании импульсного поля несимметричной полосковой линии участвуют вихревые токи, индуцированные в токопроводящей поверхности 5 (см. рис. 2.14) магнитным полем токонесущего проводника, глубина проникновения которых в металл определяется формулой (2.18). Необходимость детального определения граничных условий для различных составляющих спектра усложняет расчет.

Непреодолимые в настоящее время трудности расчета заставляют искать математические модели импульсного магнитного поля, осно-ванные на экспериментальных данных. Создание этих моделей также сопряжено с трудностями и в области измерительной техники. Требуется измерять быстроизменяющиеся поля напряженностью до 10" Э в геометрическом объеме, измеряемом десятками микрон. Это потребовало разработки совершенной аппаратуры и методики измерений [46-48].

методом полоскового зонда

Сущность зондоюго метода состоит в измерении ЭДС, наводимой в измерительном витке пробным сигналом с экспоненциально нарастающим фронтом. Виток вместе с проводящей плоскостью образует несимметричную полосковую линию. Исследуемая линия и зонд, по существу, образуют ИПТ, геометрические параметры которого могут изменяться в широких пределах, а сигнал на выходе вторичной обмотки измеряется с достаточной точностью.

Схема измерительной установки показана на рис. 2.15. Исследуемая линия / и зонд 2 расположены над проводящей поверхностью. Снимаемый с выхода зонда сигнал усиливается измерительным усилителем 4 и измеряется осциллографом 5. Зонд 2 жестко соединен р измерительным столом, позволяющим перемещать его на заданное сасстояние по осям xviy. Высота линий / и 2 в процессе эксперимента изменялась с помощью диэлектрических прокладок фиксированной толщины. Линия 1 выполнена переменной ширины. Совмещение зонда с участком линии требуемой ширины осуществлялось перемещением стола по оси у посредством микрометрического винта. •Линия / исследовалась с помощью комплекта зондов шириной

Рис. 2.15. Схема установки для исследования импульсных полосковых трансформаторов зондовым методом

И углом, под которым расположен торец зонда относительно измеряемой линии.

Относительно характера измеряе-.мого магнитного поля делались следующие допущения. Поле линии / предполагалось симметричным относительно оси у. Осевая симметрия является следствием предположения о квазистационарности поля в полосе частот от 1 до 50 МГц, где магнитное поле создается только током проводимости 1в (О и токами смещения в диэлектрике линии можно пренебречь.

Второе допущение касается временного описания магнитного поля

в некоторой точке пространства вокруг линии /. На интервале 4 временная зависимость поля предполагается аналогичной зависимости тока в линии (2.17). В обоснование данного предположения приведем следующие соображения. В формировании магнитного поля вне проводника / участвуют две составляющие: поле, создаваемое током в проводнике /, и составляющая поля, вызванная вихревыми токами в проводящей плоскости. Поле тока проводимое! и устанавливается в пространстве вокруг проводника за пренебрежимо малое время, определяемое скоростью распространения электромагнитной волны в вакууме. Поле индуцированных в проводящей подложке токов будет устанавливаться медленнее. Фазовая скорость распространения электромагнитной волны в металле Уф = (оА. Время проникновения низкочастотной составляющей спектра импульса на глубину А = 30 мкм составит 84 не, что обычно меньше периода следования импульсов тока. Следовательно, накоплением низкочастотных составляющих поля в проводящей подложке можно пренебречь и считать, что время установления вихревых токов не имеет существенного фазового сдвига в гармонические составляющие импульса магнитного поля.

Пусть на интервале времени О - плоскость витка зонда пронизывает магнитный поток, созданный током возбуждения!

4(0 = .,(1-Г ). Напряжение на выходе зонда

Амплитудное значение напряжения

В соответствии со вторым законом Кирхгофа для J

(2.19)

(2-20) I справедливо

уравнение

(2.21)

где Afj, - взаимная индуктивность шин J и 2; - индуктивность зонда; tj - ток во вторичной цепи ИПТ.

Усилитель 4 измерительной установки имеет большое входное сопротивление. Поэтому можно положить = О, тогда из (2.21) следует

или для амплитудных значений

tJ2m=M,,-. (2.22)

Приравнивая (2.20) и (2.22), получаем

Таким образом, установка позволяет найти взаимную индуктивность полосковых линий на единицу длины /о = 1 мм

Mq.21 = UzmT/IJ (2.23)

и магнитный поток или потокосцепление шины и зонда

% = Мо.2,/„. (2.24)

Заметим, что в силу непрерывности линий магнитного поля,вытекающей из четвертого уравнения Максвелла div й = О, существует возможность приравнять поток через плоскость витка зонда к потоку через пJtoщaдкy, перпендикулярную проводящей поверхности и ограниченную торцом зонда и его проекцией на проводящую поверхность. Среднее значение горизонтальной составляющей индукции магнитного ноля через эту площадку

Б=ср = Wa- (2.25)

Среднее значение вертикальной составляющей индукции через плоскость зонда

fiicp-=W3. (2.26)

где /г, - длина зонда

От значений индукции легко перейти к средним значениям напряженности поля Яср. Изменяя значение с небольшой дискретностью, можно изучить зависимость горизонтальной составляющей напряженности, поля Н от высоты линии.

Остановимся на методике измерения амплитудных значений напряжения на выходе зонда. В качестве регистрирующего прибора при измерении амплитуд импульсных сигналов целесообразно использовать широкополосный осциллограф, так как исследуемые сигналы занимают полосу до 50-70 МГц. Однако широкополосные осциллографы имеют чувствительность в несколько милливольт. При непосредственном подключении осциллографа на выход зонда чувствитель-

Рис. 2.16. Схема калибровки уста новки по коэффициенту усиления.

ность установки для измерения нап ряженности импульсных полей была бы ограничена единицами эрстед. Для увеличения точности измерений чувствительность установки потребовалось увеличить на два порядка, что было достигнуто включением усилителя 4 (см. рис. 2.15) с малым уровнем собственных шумов и высокой степенью подавления внешних помех. Такой усилитель удалось разработать, используя высокочастотные транзисторы.

Широкополосные транзисторные усилители с большим коэффициентом усиления (больше 100) имеют нелинейную амплитудную и амплитудно-частотную характеристики, т. е. коэффициент усиления по амплитуде зависим от амплитуды и длительности входного импульса. Поэтому потребовалось получить амплитудную характеристику для сигналов, форма которых практически не отличалась бы от формы сигналов, полученных с выхода зонда.

Эта задача решалась путем калибровки усилителя с помощью индуктивного делителя напряжения. Генератор импульсов тока подключался к плоской линии / с отводами (рис. 2.16). Так как активным и емкостным сопротивлениями линии можно пренебречь по сравнению с ее индуктивным сопротивлением, то напряжение на входе линии

(2.27)

и совпадает по фррме с выходным напряжением зонда. Амплитуда напряжения на входе линии через переключатель 3 измерялась осциллографом 4. Зная падение напряжения на линии, ее длину и положение отводов, легко рассчитать входное напряжение усилителя 2 при его подключении к каждому из отводов. Амплитудная характеристика усилителя получена для пробного сигнала, создаваемого током с

фронтом 10 НС.

2.7. Взаимная индуктивность полосковых линий

Важнейшей характеристикой полосковых линий является индуктивность на единицу длины L. Она зависит от ширины линии и ее высоты d. Для измерения зависимости индуктивности от этих параметров методом фотохимического травления получена линия переменной ширины с отводом для подключения измерительного усилителя. Высота линии изменялась путем выбора диэлектриков различной толщины.

Особенность измерения индуктивности линий состоит в том, что на вход измерительного усилителя наряду с напряжением U, снимаемым с участка линии длиной о. действует синфазное напряжение на отрезке линии от /о до точки заземления. Значение этого напряжения может многократно превосходить U. Для исключения его влияния на точность измерений измерительный усилитель выбран с боль-

/.„,нГн/мм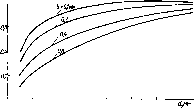

О 0,2 0,4 0,6 Цв 1,0 1,2

Рис. 2.17. Погонная индуктивность микрополосковых линий

шим коэффициентом подавления синфазной помехи. В схеме измерительного усилителя это обеспечивается благодаря использованию транзисторного генератора тока в качестве источника эмиттерного питания первого каскада, выполненного по дифференциальной схеме.

Индуктивность линий рассчитывалась по формуле (2,27) при / = = О, = 0,1 А и т = 10 НС,

Зависимость погонной индуктивности несимметричных полосковых линий от их ширины представлена на рис, 2.17. Полученные кривые при увеличении высоты линий до 10 мм сближаются и асимптотически стремятся к пределу 0,85-0,95 нГн/мм.

Полученные данные позволяют сделать важный для практики вывод об уменьшении скорости нарастания индуктивности от высоты линии. Причем это уменьшение проявляется в большей степени для линий малой ширины.

При толщине диэлектрика d = 0,02 мм изменение ширины линии от 0,6 до 0,1 мм приводит более чем к двукратному увеличению индуктивности. Сравним данные измерений с расчетными, полученными по широко используемой на практике формуле [44]

которая получена в предположении, что d < &, А = 0. Для линии d = = b = 2 • и Lo = 1,25 нГн/мм (результат измерения L, = = 0,47 нГн/мм). Имеет место рассогласование результатов в 2,6 раза. Для линии с & = 6 . 10"® м и d = 10" м расчет дает Lo = = 0,21 нГн/мм, а результат измерения Lo = 0,19 нГи/мм, т. е. наблюдается удовлетворительное совпадение результатов, поскольку в последнем случае линия имеет малую по сравнению с шириной высоту.