лам, приведенным в табл. 1.3, а и - чувствительности по току и по напряжению его электродной системы.

Механотронные акселерометры относятся к числу приборов инерционного действия [3, 37], отличительной особенностью которых является наличие инерционного элемента - так называемой инерционной массы.

Механотронные акселерометры применяются в аппаратуре для измерения и регистрации ускорений и перегрузок различных движущихся объектов (например, на транспорте, при испытании машин и аппаратов, в медицине и т. д.). При этом корпус акселерометра жестко укрепляется непосредственно на исследуемом объекте, а смещения подвижного электрода механотрона, соответствующие характеру ускоренного движения, возникают благодаря действию инерционных сил.

Механотронные акселерометры позволяют определять линейные и угловые ускорения - как постоянные, так и переменные, имеющие периодический или непериодический характер изменения. Преимущественно механотроны применяются для измерения линейных ускорений. ,

Основными параметрами механотронного акселерометра являются его чувствительности по току и по напряжению (7j;„ и 7j„a) к ускорению, которые определяются как

-nia =

да да

(2.15)

(2.16)

В соответствии с уравнением (1.2) для tj, и -ца могут быть записаны следующие выражения:

niaia (2.17)

-Пиа-иа, (2.18)

где f, и - чувствительности по току и по напряжению электродной системы акселерометра, а Оа -чувствительность к ускорению его кинематической системы, которая определяется по формулам, приведенным в табл. 1.3.

Важным параметром механотронного акселерометра является частота собственных колебаний кинематиче-ской системы акселерометра /о. У акселерометра эта

частота должна быть значительно выше частоты измеряемого переменного ускорения.

Механотронные вибропреобразователи предназначены для измерения параметров механических вибраций: частот, амплитуд и виброускорений.

Указанные параметры механических вибраций связаны определенными соотношениями, вытекающими из общей теории колебаний [35-37].

Предположим, что под действием вибрации подвижный элемент механотронного вибропреобразователя совершает простое гармоническое колебание, подчиняющееся закону

x = x,„smmt, (2.19)

где X - мгновенное значение смещения вибрирующего элемента от положения равновесия; х„ - амплитудное значение его смещения; ю - угловая частота вибрации; / - время.

Мгновенное значение ускорения а, возникающего при вибрации и действующего на вибрирующий элемент, выражается уравнением

«3= ~~ = -«.. (2.20)

а амплитудное значение этого ускорения опреде-

ляется как

а.т==х\ (2.21)

Уравнение (2.21) связывает три,основных параметра вибрации (частоту, амплитуду и ускорение) и позволяет определить любой из этих параметров, если известны два других.

Механотронный вибропреобразователь преобразует параметры механической вибрации в электрические сигналы за счет перемещения подвижных электродов механотрона относительно неподвижных. При этом вибропреобразователь должен быть соединен с вибрирующим объектом таким образом, чтобы в механотроне обеспечивалось указанное смещение электродов. Возможны два принципиально различных способа осуществления такого соединения (рис. 2.2).

В первом случае штырь механотронного преобразователя перемещений (рис. 2.2,а) соединен с вибрирующим объектом /, а сам механотрон 2 укрепляется на неподвижном основании 3. При этом колебания источ-5-1003 65

ника вибраций - объекта / через штырь механотрона передаются только его подвижным электродам, а остальные электроды механотрона и его баллон остаются неподвижными.

Теоретический анализ показывает [35-37], что в этом случае амплитуда смещений подвижных электродов механотрона будет равна амплитуде вынужденных колебаний вибрирующего объекта в области

- It

1 Z J ч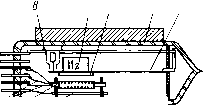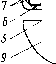

"1

Рис. 2.2. Схемы соединения вибрирующего объекта и механотронного вибропреобразователя с внещним (а), внутренним (б) управлением и конструкция механотронного акселерометра с внешним

управлением (в): о - действующее ускорение; Af - инерционная масса; Л - анод; а-перемещение конца штыря под действием инерционной силы; 4d - перемещение аиода; т и п - длина внутреиней и внешней частей стержня механотрона

частот со<Ссоо (где соо=2л/- угловая частота собственных колебаний кинематической системы механотрона). В области более высоких частот вибрации (со>соо) штырь механотрона как бы не успевает следовать за быстрыми смещениями вибрирующего объекта. При этом с увеличением частоты амплитуда смещений х„ подвижных электродов механотрона быстро уменьшается по сравнению с амплитудой вибрации г/ и стремится к нулю при частотах со>соо.

Таким образом, механотронный преобразователь перемещений в этом случае выполняет роль вибропреобразователя, который можно использовать для измерения амплитуд и частот вибраций, причем рабочей областью частот такого вибропреобразователя является ш<соо, так как лишь в этой области его сигналы пропорциональны амплитуде вибрации.

Описанный метод измерения амплитуды и частоты вибрации с помощью механотронного преобразователя перемещений, закрепленного на неподвижном основании, называется методом измерения относительно неподвижных координат [37]. Непосредственно измерять виброускорение этим методом не удается. Величину можно рассчитать, используя формулу (2.21), по измеренным л: и со.

Существенным недостатком данного метода является то, что для проведения измерений рядом с вибрирующим объектом необходимо иметь неподвижную базу, на которой должен быть закреплен механотрон. Это ограничивает возможности применения описанного метода.

Более универсальными и удобными в эксплуатации являются вибропреобразователи инерционного действия, которые измеряют вибрацию исследуемого объекта относительно инерционной массы, соединенной с объектом посредством упругого элемента.

Механотронные вибропреобразователи инерционного действия могут выполняться как с внутренним (рис. 1.3,в и 2.2,6), так и с внешним (рис. 2.2,в) механическим управлением.

Механотронные вибропреобразователи инерционного действия характеризуются в основном теми же параметрами, что и акселерометры. Однако, как будет показано ниже, важнейшим параметром вибропреобразователя, от величины которого в большой степени зависят измерительные свойства прибора, является частота собственных колебаний его кинетической системы. 5* 67

в общем случае в конструкции вибропреобразователя инерционного действия (рис. 2.2,6) должны быть предусмотрены следующие элементы: инерционная масса /, жестко связанная с электродом 2 и соединенная с корпусом .<? механотрона посредством эластичной пружины 4, электроды 5-7 (анод 5, катод 6 и подогреватель 7), жестко связанные с корпусом 5 механотрона, успокоитель & (например, электромагнитного типа). При измерении параметров вибрации корпус вибропреобразователя жестко укрепляется на вибрирующем объекте 9.

В процессе вибрации корпус 3 вибропреобразователя и связанные с ним электроды 5-7 вибрируют, т. е. совершают вынужденные колебания с частотой источника вибрации. При этом благодаря действию инерционных сил масса / и связанный с нею электрод 2 не успевают следовать за быстрыми смещениями вибрирующего корпуса механотрона и остаются практически неподвижными в пространстве. В результате этого в вибропреобразователе происходит относительное смещение электродов, связанных с корпусом механотрона, и электродов, связанных с инерционной массой. В дальнейшем электроды, жестко связанные с инерционной массой, мы будем называть подвижными электродами механотрона.

Движение кинематической системы вибропреобразователя, которая образована инерционной массой /, подвижным электродом 2, пружиной 3 и успокоителем 8, описывается следующим дифференциальным уравнением [37J:

М -т- + N

+ Lx=0,

(2.22)

где М - величина инерционной массы; х - перемещение инерционной массы и связанного с ней электрода относительно вибрирующего объекта; z-абсолютное перемещение инерционной массы и связанного с ней электрода в неподвижной системе координат, причем z = x+y {у - перемещение вибрирующего объекта в неподвижной системе координат); Л - коэффициент успокоения {Ndx/dt -ста успокоения); /.= 1/ожесткость пружины {Lx - сила упругости).

Отметим, что при составлении уравнения (2.22) были приняты некоторые упрощения, вполне допустимые для механотронного вибропреобразователя. Так, было 68

принято, что перемещение х инерционной массы (подвижного электрода) очень мало и характеристика кинематической системы в этом диапазоне перемещений- линейна, т. е. сила упругости пружины F пропорциональна перемещению x(F = Lx). Принято также, что в вибропреобразователе отсутствуют другие силы трения, кроме сопротивления, создаваемого успокоителем, причем величина этого сопротивления прямо пропорциональна скорости перемещения инерционной массы (Ndx/dt). Кроме того, при составлении уравнения (2.22) массой подвижного электрода и пружины по сравнению с величиной инерционной массы М пренебрегают.

Заменяя в уравнении (2.22) z на х+у, получаем

М +NLxM.y

(2.23)

dt dt df

Разделив все члены уравнения (2.23) на Af и введя обозначения N\M. = 2 и ЦМ. = (а\, получим уравнение движения кинематической системы вибропреобразователя в виде

dx , „Q ал; , „ de dt

dPy dt

(2.24)

где 2p -приведенный коэффициент успокоения; соо - частота собственных колебаний системы.

В этом уравнении х, равное перемещению подвижного электрода механотрона относительно его неподвижных электродов, будет соответствовать показаниям вибропреобразователя, а у - перемещению исследуемого объекта.

Используя уравнение (2.24), можно качественно показать, какими должны быть параметры вибропреобразователя, чтобы он соответствовал тому или иному назначению. Если в вибропреобразователе отсутствует успокоитель (2§~0), а соо<(о, то уравнение (2.24) примет следующий вид:

d-x flfzy dt df

С точностью до произвольных постоянных решение этого уравнения можно представить в виде

а: = -У,

причем х = у. (2.26)

(2.25)