
 |
|
Главная страница Алгебраическая теория кодирования [0] [1] [2] [3] [4] [5] [6] [7] [8] [ 9 ] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] где Xi,-j заданы для всех г, / = О, 1, . 1, а Z„, Zi, Zm i ДОЛЖНЫ быть определены. В матричных обозначениях эта система может быть записана в виде ZX = О, где левая часть есть сокращенная запись произведения -1 -1
m-l, m-l-" Уравнение ZX = 0 означает, что скалярное произведение вектора Z и каждого из столбцов матрицы равно 0. Это свойство сохраняется, если поменять местами любую пару столбцов матрицы X, или прибавить некоторый столбец матрицы X к любому другому ее столбцу, или умножить произвольный элемент матрицы X на ненулевой скаляр. Так как каждая из этих операций над столбцами обратима, то можно выполнять любую комбинацию этих операций над: столбцами в любом порядке. Такие операции над столбцами не долж- ны изменять вектор Z, являющийся решением системы. С помощью подходящих операций над столбцами матрица X может быть приведена к одной из известных канонических форм.!. Для наших целей наиболее подходящей является приведенная тре- угольная идемпотентная форма, обозначаемая через X. Эта форма! определяется следующим образом: 2.51. Определение, {т X т)-матрица X имеет приведенную треугольную идемпотентную форму, если каждый ее элемент, расположенный ниже главной диагонали, равен нулю, каждый эле- мент главной диагонали равен нулю или единице, каждый элемент, в столбце которого имеется нуль главной диагонали или в строке которого имеется единица главной диагонали, равен нулю ). Следующая матрица является примером треугольной идемпс тентной матрицы над GF (5): 0 2 4 0 3 1 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 2 3 0 0 0 0 1 0 О О О О О и В символической записи это означает, что Xi, j - О, если i > Ц Xi, j = О или 1, если i = j, и Xt, j = О, если Xt, t = 1 или eci 1) Приведенная треугольная идемпотентная матрица имеет те же столбцы что и более общая стандартная эпсилон-матрица, но столбцы ее упорядочев-другим образом. Xj, у = О, Иначе, Xt, j О, только если Xj, • = 1, и либо i = /, либо i <С i vi Xi, I = 0. Термин треугольный вытекает из требования Xi, j = при i > /. Термин идемпотентный объясняется следующей теоремой: 2.52. Теорема. Всякая квадратная матрица в приведенной треугольной идемпотентной форме удовлетворяет уравнению Х = = Х. Доказательство. Элемент Xt, j отличен от нуля только тогда, когда Xj,j = 1; элемент Xj, и отличен от нуля только тогда, когда / = к или / < /с и Xj, j = 0. Поэтому произведение Xi, j Xj, k равно нулю во всех случаях, кроме j = к. Следовательно, S i, jj, h =Xi, kXk, ft- Если Xk, ft = 0, TO Xi, k = 0; если Хн, k Ф О, то Xk, k = i-В любом случае Xi, h Xk, k = Xi, h 2j Xi, jXj, k - Xi, ft для всех ink. Это эквивалентно матричному уравнению Х = X. щ Из этого результата следует простая характеристика вектор-строк Z, удовлетворяющих уравнению ZX = 0. В дальнейшем нам также понадобится характеристика вектор-строк U, удовлетворяющих уравнению VX = U. Теорема формулируется следующим образом: 2.53. Теорема. Если X-приведенная треугольная идемпотентная матрица, то Z является решением уравнения ZX = О тогда и только тогда, когда Z есть линейная комбинация строк матрицы X ~ J, где J - единичная .матрица. Аналогично U (. - J) = О тогда и только тогда, когда вектор U есть линейная комбинация строк матрицы X. Вектор U является такой линейной комбинацией тогда и только тогда, когда произведение каждой координаты U и соответствующего диагонального элемента матрицы X - 3 равно нулю. Доказательство. Если Х = X, то Х - X = Q ж {X - - 3) X = 0. Следовательно, если Z - произвольная линейная комбинация строк матрицы X -J, то ZX = 0. Аналогично, если i = X, го Х- ~ X = О и X {X - 3) = 0. Следовательно, если U - линейная комбинация строк матрицы X, то U удовлетворяет уравнению и (i? - J) = 0. Так как только ненулевые столбцы матрицы X - О имеют на главной диагонали -1, то ранг матрицы X - J равен дефекту X. Следовательно, линейные комбинации строк матрицы X - 3 исчерпывают все решения уравнения ЪХ = 0. Так как все ненулевые столбцы матрицы X имеют на главной диагонали 1, то ранг матрицы X равен дефекту матрицы X - О- Следовательно, линейные комбинации строк X исчерпывают все решения уравнения U {X - CI) = 0. Произведение канедой координаты вектора U на соответствуюн],ий диагональный элемент матрицы X - J равно нулю тогдаи только тогда, когда нулевой координате U соответствует нулевой столбец матрицы X. Так как каждый ненулевой столбец треугольной матрицы X имеет на главной диагонали единицу, то U является линейной комбинацией строк матрицы X тогда и только тогда, когда каждому нулевому столбцу из X соответствует нулевая координата U. щ Наконец, докажем теорему 2.54. 2.54. Теорема. Любая квадратная матрица с помощью операций над столбцами может быть приведена к треугольной идем-потентной форме. Хотя суш;ествует несколько способов такого приведения, мы остановимся не на самом простом, а на наиболее просто реализуемом," Рис. 2.20. Циклический сдвиг столбцов влево. Рис. 2.21. Циклический сдвиг строк вверх. Так как допустима перемена мест для любой пары столбцов то столбцы можно переставлять в любом необходимом порядке. Соот ветственно определим операцию «циклического сдвига столбцов влево» с помош;ью диаграммы, приведенной на рис. 2.20. Аналогично с помош,ью диаграммы на рис. 2.21 определим операцию «циклического сдвига строк вверх». Бдительный читатель в этом месте должен насторожиться: допустимой является операция перестановки столбцов, а не строк. Однако рассматриваемая процедура использует операцию сдвига строк траз, так что в итоге строки располагаются в первоначальном порядке. А так как операция сдвига строк перестановочна со всеми операциями над столбцами, то т циклических сдвигов строк вообш;е не оказывают никакого влияния. Зачем же тогда вообш;е нужны сдвиги строк? Затем, что некоторые решающие правила процедуры зависят от .шачений элементов в определенных строках и технически осуществлять эти правила с помощью сдвигов строк оказывается намного легче, чем с помощью специальной, достаточно тонкой аппаратуры, анализирующей каждую строку матрицы. 2.55. Алгоритм приведения матрицы (к треугольной идемнотентной форме). Процедура состоит из следующего базисного множества шагов, повторяющегося т раз: 1. Не делать ничего, если верхний член первого столбца матрицы отличен от нуля. Если верхний член первого столбца равен нулю, то поменять местами первый столбец с самым левым столбцом, в котором верхний элемент отличен от нуля, а элемент главной диагонали равен нулю. Если такого столбца нет, то поменять местами первый столбец с самым левым столбцом, в котором верхний элемент и элемент главной диагонали отличны от нуля. Если и такого столбца нет (в этом случае верхняя строка является нулевой), то не делать ничего. 2. Разделить все члены первого стобца на верхний элемент. (Если этот элемент равен нулю, не делать ничего.) 3. Аннулировать верхние элементы всех столбцов, кроме первого, с помощью вычитания подходящего кратного первого столбца. 4. Сдвинуть циклически строки вверх, а столбцы влево. В двоичном случае шаг 2 можно опустить. Каждый из остальных шагов выполняется в один временной цикл. Блок-схема для выполнения операции 1 объяснена на рис. 2.22 и 2.23, а для операции 3 - на рис. 2.24. В общем случае после /с-кратного выполнения множества базисных шагов первые т - к столбцов матрицы содержат нули в нижних строках и нижняя правая (к X А;)-подматрица является треугольной идемнотентной. Читателю предлагается проверить это утверждение, используя индукцию но к. Пусть, например, (7 X 7)-матрица над GF (5) после четырехкратного выполнения базисных операций 5-658 имеет вид О 2 О О ООО 0 0 0 0 0 0 0 0 0 0 3.4 1 ООО 3 2 1 О 0 0 0 0 0 0 Верхний символ Диагональный символ Рис. 2.22. Подробная блок-схема одной, ячейки из рис. 2.23. Вход Авх равен 0 тогда и только тогда, когда верхняя координата наиболее левого столбца равна! 1, а его диагональный элемент равен 0. Если в данном столбце в верхней позиции стоит 1, а на диагонали стоит О, то выход Л оыж полагается равным 1, в противном случае Л выж равно Авх- Вход Вех равен О тогда и только тогда, когда все А рав-1 ны О и ни один из более левых столбцов не имеет нулевой верхней координаты.! Если любой из сигналов А или В изменяет свое значение с О на 1, то в точ-< ках D или С появляется соответственно сигнал 1 и выход Е принимает значе ние 1, указывающее на то, что данный столбец надо поменять местами с крайни* левым столбцом. Связи между столбцами показаны на рис. 2.23. Заметим, что распространв! ние сигнала вдоль линий А ъ В и изменение его с О на 1 затрагивает только столбец, который должен переставляться. Если элемент в верхнем левом угл5 равен 1, то этот сигнал всюду равен 1; если каждый элемент верхней строки равен О, то и сигнал всюду равен 0. Обоим этим случаям соответствует отсут-jl ствие каких-либо перемен, и анализируемый столбец не надо переставлять с крайним левым столбцом. Реализация перестановки столбцов требует многих элементов, не показав ных на схеме. Ее можно осуществить хотя и громоздким, но прямым способом использующим сигналы Е в качестве управляющих сигналов для перестановк! столбцов. 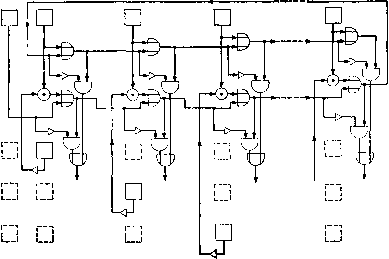 Р и с. 2.23. Схема для выбора столбца двоичной матрицы, переставляемого с первым столбцом. □ Р и с. 2.24. Схема для выполнения над двоичной матрицей операции «превратить в нуль верхний элемент каждого столбца (за исключением крайнего слева) путем вычитания подходящего кратного крайнего левого столбца». [0] [1] [2] [3] [4] [5] [6] [7] [8] [ 9 ] [10] [11] [12] [13] [14] [15] [16] [17] [18] [19] [20] [21] [22] [23] [24] [25] [26] [27] [28] [29] [30] [31] [32] [33] [34] [35] [36] [37] [38] [39] [40] [41] [42] [43] [44] [45] [46] [47] [48] [49] [50] [51] [52] [53] [54] [55] [56] [57] [58] [59] [60] [61] [62] [63] [64] [65] [66] [67] [68] [69] [70] [71] [72] [73] [74] [75] [76] [77] [78] 0.0115 |