Если требуется умножить записанный в регистре элемент Y на1 элемент а, то надо построить схему, умножающую на матрицу

-001011 1 0 0 0 0 laj = 0 10 0 0 0 0 10 0 L0 О О 1 0J Такая схема приведена на рис. 2.12.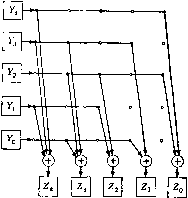

Рис. 2.12. Схема для умножения на а.

Y4 -1 Уз -1 Уг -1 Ухп Уо-,

U /з W 2 (+).. Zi L Z

Рис. 2.11. Схема для умноже-

Р и с. 2.13. Схема для умноже-

ния на а"

ния на а".

-11 -

Аналогично, если произвольный элемент Y, записанный в реги стре, требуется умножить на элемент а", то надо построить схему умножающую на матрицу

ГО 1 О О О 0 0 10 0 0 0 0 1 0 0 0 0 0 1 L1 О О 1 0J

Такая схема изображена на рис. 2.13.

Обозначим через W (М) вес многочлена М (х), т. е. число ei ненулевых коэффициентов. Если поле задано с помощью корня многочлена М (х), то для умножения регистра на элементы а ил1

требуется в общем случае всего W (М) - 2 сумматоров с двз входами. Для многих значений т удается построить ненриводимы двоичные многочлены степени <т, вес которых равен 3 ). В это1

) Дальнейшее исследование неприводимых двоичных многочленов с ве 3 можно найти в § 6.3.

случае умножение на а или может быть выполнено с помощью только одного сумматора с двумя входами.

2.42. Умножение двух «регистров». Рассмотрим произведение Z = UV двух элементов ноля U п V, записанных в регистрах памяти. Каждая из т компонент этого произведения

I- 4

Рис. 2.14. Схема для умноже- Рис. 2.15. Схема циклического ния и на а. сдвига V вправо.

является линейной комбинацией двоичных произведений UfVj. Следовательно, эта операция записывается с помощью {т X т X X /ге)-тензора. Такое умножение может быть непосредственно реализовано с помощью метода, предложенного Бэрти и Шнейдером [1963]. В зависимости от вида неприводимого многочлена эта реализация

г- Z.

г- Zp

Рис. 2.16. Схема для прибавления кратных U к Z.

многочлена требует порядка - т сумматоров с двумя входами. Даже при хорошем выборе неприводимого многочлена столь большое число сумматоров с двумя входами делает эту процедуру чрезвычайно дорогой для больших тп. Если нет необходимости в максимальной скорости вычислений (один временной цикл, гарантируемый методом Бэрти - Шнейдера), то предпочтительней более длительные, но менее дорогие способы умножения. Одним из таких способов является следующий метод умножения, очень близкий к методу, Н)едложенному Питерсоном [1961].

Пусть множитель U записан в регистре с обратной связью, позволяющей но команде заменять U на а?7. Пример такого регистра для корня а многочлена М {х) = х + х -\- i приведен на рис. 2.14. ЙЬтожитель V запоминается в регистре, в котором можно осуществить ннклический сдвиг вправо, как показано на рис. 2.15. Произведение Z накапливается в регистре, к содержимому которого можно прибавлять содержимое /-регистра, как показано на рис. 2.16.

Начальное состояние Z-регистра является нулевым. В зависимости от значения низшего разряда Fq множителя V множитель U прибавляется или не прибавляется к Z. Если = 1, то С/ прибавляется к Z; если Vq = О, то Z остается без изменений. После этого F-регистр сдвигается вправо, [/-регистр умножается на а и процесс повторяется. На тг-м шаге умножения вместо U записано aU, вместо

Fo записано F„ и Z-регистр содержит 2 {Щ- После т таких

шагов умножение закончено и Z-регистр содержит произведение исходных U- и F-регистров. При этом Z-регистр циклически сдвинут в свое исходное положение, а [/-регистр содержит a™-U. Поэтому если для дальнейших вычислений требуется восстановить первоначальный вид множителя U, то нужно добавить дополнительную схему. Исходный вид множителя можно восстановить в один шаг с помош,ью схемы умножения на константу а"*™-**. Зачастую, однако, эта операция требует так много дополнительных сумматоров, что оказывается дешевле построить специальный регистр для запоминания первоначального состояния U.

Более дешевым методом восстановления исходного состояния регистра множимого является т-кратное умножение на константу а~. Если вес М (х) равен 3, то такая процедура, хотя и требует т временных циклов, использует всего один сумматор с двумя входами. Возможны также и вариации этого метода, как, например, умножение на а и сокращение необходимого времени до т/2 временных циклов. Другим возможным решением является осуществление умножения [/-регистра на а, и а и сдвигов F-регистра сразу на две позиции вправо и влево и на одну позицию вправо. При этом произведение можно накапливать в Z-регистре согласно правилу

Z = VoU + F2 (С/а*) + F4 (С/а*) + • • • + Vm-i (Ua"") +...

...+V, {Ua) + Vs (С/аЗ) + F, (Ua).

Такой метод умножения позволяет получать произведение за т] шагов и восстанавливать исходное состояние регистров множителей! за один или два дополнительных шага. Однако он требует несколько! более сложной управляющей логики.

2.43. Таблицы логарифмов. В качестве последнего] метода выполнения операций умножения, деления, возведения в сте- пень и извлечения корня рассмотрим использование таблиц логариф-! мов. Такие таблицы могут быть построены для ненулевых элементов в любом поле. Например, если а - корень неприводимого двоичного многочлена М (х) = х х + i, то умножение на а может быт1 выполнено с помощью регистра сдвига с обратной связью, изобра-! женного на рис. 2.17. Отправляясь от начального состояния регистра

1 = Оа* -Ь Оа* + Оа -- Оа + 1, можно получить все степени а как соответствующие состояния этого регистра сдвига. Первые 31 сте пени будут совпадать со всеми 31 ненулевыми элементами поля (ai = = а" = 1). Следовательно, каждый ненулевой элемент этого поля можно представить как степень а и построить, таким образом, таблицы логарифмов и антилогарифмов, приведенные в приложении А.

Рис. 2.17. Регистр сдвига с обратной связью для умножения на а.

Использование подобных таблиц сильно упрощает ручное вычисление произведения, частного, степеней и извлечение корней для элементов поля. Например, рассмотрим произведение

1а* + Оа» + 1а2 1а + О = 10110 = а

Оа* -f Оа» -L 1а2 + Оа + 1 = 00101 == а

частное

10110

= а2 = 00100,

= а23 = 01111,

00101

степень

(10111)8 = (а2«)в = (а-5)б = а-з« = а = 00010

и корень

(11001)/* = (а25)/ = (а25)8 = «200 (31-6+14 = а"-11101,

так как 4.8 = 1 mod 31.

В общем случае построение таких таблиц возможно тогда и только тогда, когда каждый ненулевой элемент поля является степенью одного, так называемого примитивного элемента. В теореме 4.24 мы докажем, что каждое конечное поле содержит такой элемент. Следовательно, подобные таблицы логарифмов и антилогарифмов могут быть построены для любого конечного поля.

Хотя таблицы такого рода являются чрезвычайно полезными при ручных вычислениях, их ценность для машинного счета весьма сомнительна. Действительно, одним очевидным методом реализации машинных вычислений с помощью таких таблиц является использование двух устройств постоянной памяти, содержащих по 2"* - 1 Слов из т двоичных цифр: одно устройство памяти должно содержать логарифмы, а другое - антилогарифмы. При этом все операции умножения и деления сводятся к последовательным сложениям и вычитаниям показателей по модулю 2" - 1. К сожалению, для больших значений т число двоичных разрядов в такой памяти растет

как т (2"" - 1), и для многих приложений это оказывается значительно дороже, чем прямой метод, описанный в разд. 2.42.

Если известен некоторый метод, позволяющий легко вычислять логарифмы элементов ноля (основанный не на просмотре таблиц, а на операциях над координатами двоичных представлений элементов ноля в виде многочленов от а), то логарифмический подход может составить основу экономной реализации операций умножения и деле- ; ния. В общем случае, однако, не известно никаких простых методов непосредственного вычисления логарифмов. Некоторые очень частные! результаты в этом направлении содержатся в задачах 4.3 и 4.4.1

2.44. Квадраты и квадратные корни. Другим] частным случаем умножения, заслуживающим отдельного рассмотре-] ния, является умножение элемента ноля, записанного в регистре YA на самого себя, Z = Y". Так как с помощью регистров сдвигов мы! умеем выполнять операцию умножения вектор-строки на матрицу, то в принципе мы можем реализовать любую линейную операцию! над элементами поля. В частности, это относится и к такой операции,, как возведение в квадрат. Для большинства полей возведение! в квадрат не является линейной операцией. Однако в нолях, содер-! жащих двоичное поле, всегда выполняется равенство (Р -\- уУ = = + 7, и, следовательно, в этом случае возведение в квадрат - линейная операция, и квадрат любого элемента ноля может быть! представлен в виде соответствующей линейной комбинации квадратов! базисных элементов. Например, если а - корень многочлена +Г + + \, то

(а*)2 = а« = аа = а» (а + 1) = + а» = а» -Ь -Ь 1, (аЗ)2 = а" = аа = а (а + 1) = а* + а, {aY = а\ {aY = а\ (а») = 1,

так что преобразование Z = может быть вычислено как Z = YcS"! где

-0 110 1-0 10 10 S= 1 0 0 0 0 0 0 10 0 LO о о о и

Это матричное умножение может быть выполнено с помощью схемы приведенной на рис. 2.18. Обратная матрица имеет вид

0 0 1 0 0-] 10 0 11 с5-1 = 0 0 0 1 0 110 11 L0 О О О 1.

Очевидно, что извлечение из элементов поля квадратного корня может быть осуществлено путем умножения на эту матрицу. Таким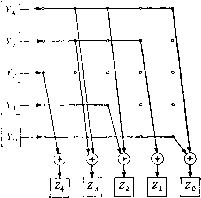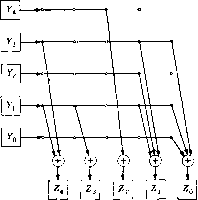

Р ц с. 2.18. Схема для вычисления Рис. 2.19. Схема для вычисления Z=y2 mod (х5 + а:2 + 1). 7 = УУ mod (х + + 1).

образом, преобразование Z = может быть представлено в форме Z = Yc- и реализовано с помощью схемы, изображенной на рис. 2.19.

*2.Ъ. Решение систем линейных уравнений

В последних главах мы видели, что некоторые задачи, возникающие в теории кодирования, могут быть сведены к решению систем линейных уравнений. Часто эти системы рассматриваются над двоичным нолем. Однако в некоторых случаях приходится рассматривать другие поля, как, например, GF (5), - поле классов вычетов по модулю 5. Сложение и умножение в GF (5) задаются таблицами

Рассматриваемые системы линейных уравнений могут быть записаны в виде

<0. J-O "Ь 01 + • • • + <m-l, oZm-i ~ О, 0, 10 + <55i, i2j -- . . . -j- Xm-l, im-i = 0,