В кодере для кодов другого типа, так называемых сверточных или\ рекуррентных кодов, поступающие символы разбиваются на блоки! большой (а не малой, как в предыдущем случае) длины к. После] получения из источника к символов кодер передает п символов,! которые зависят не только от этих к символов, но и от многих paneel полученных символов. Точнее, если входом кодера была последова-] тельность данных [над GF {q)\

/(1) /( li , 1 i

jih) Ai) r(2) r(h) ,(1)

1 i , i2 ,1-1 , .... -2 , 1г ,

TO выходом кодера является последовательность где

если 1 <; / <: /с.

г ,

Й т

I S Н\%11п, если k<j<n.

l=i ft=0

(Предполагается, что /iij = 0, если Как и в случае линейных

блоковых кодов, будем обозначать через Ri полученные символы,] а через = - Ci - ошибки в канале. Для j = к+ I, к-2, . .., га определим символы синдрома с помощью равенств

h т

г = 1 h=o

Ясно, что

Многочлены

l=ih=0

l = i h=0

назовем проверочными многочленами кода. (Некоторые авторы назы- вают их порождающими многочленами.) Память кодера равна т бло- кам; кодовым ограничением называется число N = п (т -\- 1). Кодо- вое ограничение для сверточного кода, грубо говоря, играет ту же роль, что и блоковая длина для блокового кода.

Сверточные коды впервые рассматривались Элайесом [1955]. Крс ме этого, их и.зучали Хегельбергер [1959], Месси [1963], Вайне и Эш [1963], Саллайвен [1966], Редди [1968] и др.

15.62. Пример (Хегельбергер [1959]). Пусть q = 2; R = 1/2, к = 1, ?г == 2, (у, z) = у {i + z- + + z«). Память равна

шести блокам; кодовое ограничение равно 14. Кодер для этого кода показан на рис. 15.10.

Источник

данных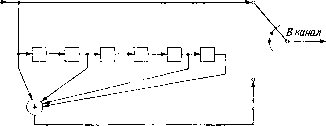

Рис. 15.10. Кодер для сверточного кода.

15.63. Пороговое декодирование. Сравнение прямого декодирования и декодирования с обратной связью. Среди проверочных уравнений,

которым удовлетворяет уравнения

код предыдущего примера, содержатся

"11001010000001 0011001010000 0000011001010 L0000001100101J

Так как эти проверочные уравнения ортогональны на £ то этот 1;од может быть декодирован с помощью порогового декодера, показанного па рис. 15.11. Полученный из канала информационный символ Rf поступает в регистр сообщения. Поступающий из канала

)1роверочный символ прибавляется к Sbj-l-j и запоминается

в регистре синдрома. При подходе к выходу из буфера сообщения лгажоритарный ) элемент выбирает символ голосованием по

большинству среди символов синдрома Sf\ Sf \, Sf , Если

Т1Ш или четыре из них равны 1, то и принимается равным 1; если менее чем два равны 1, то полагаем = 0. Декодер сможет правильно декодировать символ, если в 26 последовательных позициях R?-\ -1-6 • • произойдет не более трех ошибок. Описан-

)т]>1й декодер называется прямым, поскольку решение о символе ЕР принимается в результате анализа полученной конечной последовательности символов без учета прошлой работы декодера.

1) Мажоритарный элемент (MDE) -это пороговый элемент, порог которого liaDBH половине числа его входов.

Другой тип декодера, так называемый декодер с обратной сея зъю 1), получается из прямого декодера путем добавления в регист синдрома об1)атных связей (пунктирные линии на рис. 15.11). Новый связи позволяют исправлять ошибки не только в информационныз символах, ио и в символах синдрома. Это позволяет увеличить вероят1 ность правильного декодирования последовательных символов. Так нап])имер, если декодер с обрапгой связью, показанный на рис. 15.11J правильно нашел Ef!,Ef2, . . ., fiJLi, го символ ЕР зависит только от 14 последовательных символов Rf\ Rf\ Rui, Есл1

Из канала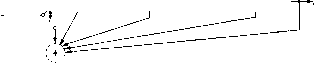

Кпотребителю данных

-(±HIh-<iKM:H3r<t>-CbDi

Рис, 15.11. Пороговый декодер для кода с рис. 15.10. (Прямой декодер полу чается из декодера с обратной связью, если опустить обозначенную пунктирмг

связь.)

среди этих 14 символов искажено не более двух и декодер с обратно! связью ранее не ошибался, то символ Ef будет правильным. Однак если декодер с обратной связью декодировал символ ненравильно то эта ошибка может привести к неправильному декодировании целой последовательности символов. Этот эффект распространень ошибки пе возможен в прямом декодере, поскольку текущие оценкя прямого декодера не зависят от прошлых ошибок.

Используя метод проб и ошибок, Месси [1963] нашел много свер точных кодов, к которым применимы простые пороговые декодер! аналогичные изображенному на рис. 15.11. Используя более систе магические методы, основанные па разностных множествах Роби! сон и Бернстейн [1967] и Редди [19(58] нашли еще много дополнител! ных кодов этого типа.

1) Этот термин, введенный Робинсоном [1967] и Гедди [1968] для обозначе ния обратных связей внутри декодера, не следует путать со схемой кодировав" - декодирования, допускающей обратные связи от декодера к кодеру.

2) Придирчивый читатель может заметить, что показатели переменного {О, 2, 5, 6}, в многочлене примера 15.62 образуют совершенное простое раз постное множество по mod 13,

Хотя пороговое декодирование оказалось очень эффективным ,11 я декодирования многих частных кодов с малым и умеренным кодовым ограничепиелг, оно представляет собой весьма слабый метод Кодирования кодов с большим кодовым ограничением. Месси [1963] оказал, что вероятность ошибки для лучших пороговых декодеров 1:с;?ависимо от длины кодового ограничения отлична от нуля.

15.64. Отыскание «хороших» с в е р т о ч п ы х к о -д о в. Все известные алгебраические процедуры декодирования для блоковых кодов основаны на ряде сведений о математической структуре этих кодов. К сожалению, среди известных сверточных кодов лишь очень немногие обладают известной структурой. Берлекэмп 11963] построил класс сверточных кодов с хорошо обозримой структурой, исправляющих пакеты стираний; однако эти коды не очень ;ффективны для каналов без памяти со случайными ошибками. Пайнер и Эш [1963] построили класс сверточных кодов, исправляющих одну ошибку при минимальном возможном защитном интервале. .)ти коды аналогичны блоковым кодам Хэмминга, исправляющим одну ошибку. К сожалению, сверточные аналоги БЧХ-кодов, исправляющих несколько ошибок, пока не известны. Эпштейн [1958 Ь] и Бассгенг [1965] нашли «лучшие» двоичные сверточные коды для некоторых скоростей передачи и малых кодовых ограничений, однако для Л > 32 подобных результатов нет.

Несмотря на то что о методах построения «хороших» сверточных кодов почти ничего не известно, многое известно о «наилучших» сверточных кодах. Эти результаты получены на основе исследования случайно выбранных сверточных кодов. Элайес [1954] показал, что такие коды позволяют получать произвольно малую вероятность ошибки декодирования при всех скоростях, меньших пропускной способности канала. Месси [1963] показал, что для сверточных кодов справедлива граница, аналогичная границе Гилберта для блоковых кодов (см. разд. 13.7). Юдкин [1964] и Витерби [1967] получили точные границы вероятности ошибки для таких кодов. Результаты Витер-он показывают, что вероятность ошибки для случайно выбранного (порточного кода с большой скоростью и кодовым ограничением Л существенно меньше, чем вероятность ошибки для лучших блоковых нодов с длиной N ).

15.65. Последовательное декодирован и е. Помимо порогового декодирования и нескольких других конструктивных методов, к сверточным кодам применим важный метод декоди-

) Точнее, результат Витербп получен при условии, что допустимы беско-14чные задержки декодирования. Если же снять это допущение, то, как показал 1. С. Ппнскер («Границы вероятности и числа псправляемых ошибок для небло-iiiibix кодов», Проблемы передачи информации, № 4, 1967), вероятность ошибки Для сверточных кодов асимптотически при N оо ведет себя так же, как II вероятность ошибки для блоковых кодов.- Прим. перев.

рования, известный под названием пос.гедовательного декодирования.] Введенный Возенкрафтом и Рейффеном [1961], этот алгоритм был] вскоре модифицирован и улучшен Фано [1963].

Конструктивные методы декодирования всегда опираются на i математическую структуру кода, а последовательное декодирование - вероятностный алгоритм, почти всегда пригодный для почти всех случайно выбранных сверточных кодов. Грубо говоря, при после-] довательном декодировании производится попытка принять решение! для каждого полученного символа, но при этом учитываются ранее] принятые решения. Если при декодировании последовательности сим-j волов на некотором шаге невозможно сделать разумный выбор, то! декодер возвращается назад и изменяет некоторые из ранее принятых решений.

Последовательный декодер Фано [1963] декодирует сверточный! код с бесконечным кодовым ограничением. При этом с вероятностью! единица любой данный символ будет в конце концов декодирован] правильно и с некоторого момента будет оставаться неизменным. К сожалению, число операций, необходимых для декодированш любого данного символа,- случайная величина, зависящая от шума в канале. Полученные Джекобсом и Берлекэмпом [1967], а также Джелинеком ) [1968[ границы показывают, что распределение это1 случайной величины примерно описывается равенством

Рг (число вычислений L) « L-P,

где р - функция от скорости передачи и статистики шума в канале Если скорость достаточно мала, то р > 1 и среднее число вычисле- ПИЙ на декодируемый символ ограничено. Однако сама случайная величина может принимать бесконечные значения. Даже в случа конечной дисперсии число вычислений для декодирования данного символа часто бывает очень большим. Именно эта проблема вычисле- НИИ, а не вероятность ошибки, ограничивает возможности после-! довательного декодирования.

Некоторые нежелательные свойства распределения числа вычис- лений при последовательном декодировании можно исключить с помо- щью гибридных схем декодирования, сочетающих сверточные кодь и последовательное декодирование с другими способами кодирова-] ПИЯ и декодирования. Такие схемы были предложены Пинскеро! [1965] и Фэлконером [1967].

Подробное исследование последовательного декодирования мож- но найти у Возенкрафта и Дн<екобса [1965] или у Джелинека [1968]. j

15.66. Сверточные коды для исправлени пакетов ошибок. Хотя для канала без памяти со случайны!

1) Граница Джелинека основана на лемме Юдкпна [1964]; частный случа этой границы был получен Сэведжем [1967а, Ь] и Фэлконером [1967].

ми ошибками не известны методы построения лучших сверточных кодов, предложены точные методы построения лучших сверточных кодов, исправляющих пакеты ошибок.

При передаче информации по некоторым каналам связи наблюдаются длинные периоды, в течение которых сигнал замирает. Такой фединг приводит к стиранию последовательных символов, что называется пакетом стираний. После окончания пакета стираний опять наступает возможность передачи информации по каналу связи без ошибок и стираний до тех пор, пока следующий глубокий фединг не Н1шведет к новому пакету стираний. Система кодирования для такого канала должна исправлять каждый пакет стираний до тех пор, пока не начнется новый пакет. Если за пакетом стираний из Е символов следует правильный отрезок сообщения из Q символов, то исправления будут не возможны, если число проверочных символов, входящих в защитный интервал, будет меньше числа стертых информационных символов. Отсюда следует, что скорость кода должна быть столь малой, чтобы выполнялось неравенство ER (2 (1 - R). Берлекэмп [1963] показал, что для любого заданного R можно пост-])оить сверточный код с величинами Е ш R, удовлетворяющими этому неравенству. В двоичном случае эта конструкция приводит к единственному коду с такими свойствами. Он допускает очень простой алгоритм декодирования, основанный на структуре кода. Оптимальные сверточные коды с исправлением пакетов стираний оптимальны также и для обнаружения пакетов ошибок максимально возможной длины.

Первая попытка построения сверточных кодов, исправляющих пакеты ошибок, была сделана Хегельбергером [1959]. Вайнер и Эш [1963] больше математизировали задачу и для лучших сверточных кодов с данной скоростью вывели границы для минимальной величины защитного интервала между исправляемыми пакетами стираний.

Берлекэмп [1964а] и Препарата [1964] построили затем класс кодов, достигающих границы Вайнера - Эша для пакетов с заданным фазовым расположением относительно блоков сверточного кода. Месси [1965] предложил простой алгоритм декодирования этих кодов. Экономи [19651 и Сю [1969] построили некоторые сверточные коды, исправляющие пакеты с меньшими фазовыми ограничениями по сравнению с кодами Берлекэмпа - Препараты. Однако общие методы построения фазово-независимых сверточных кодов, исправляющих пакеты ошибок и удовлетворяющих границе Вайнера - Эша, пока не найдены.

Галлагер [1966[ показал, что граница Вайнера - Эша применима не только к сверточным, но и к блоковым кодам. Он также построил класс сверточных кодов, исправляющих многие (по не все) пакеты заданной длины при значительно меньшем защитном интервале, чем требуется согласно границе Вайнера - Эша.