ВХОД выполняется в виде проволоки, обернутой вокруг тора опре- деленное число раз. Ток проходит по каждому входному проводу! (во всех проводах в одном направлении) тогда и только тогда, когда соответствующий ему вход равен 1. Дополнительный провод имеет! в Т раз больше витков, чем каждый из входных. По нему всегда; проходит ток в противоположном направлении. Выход порогового элемента определяется направлением потока в торе.

Декодер рис. 15.7 отличается от декодера рис. 15.6 тем, что поро- говый элемент с девятью входами заменен на несколько донолнитель-:

(+>- о 1

fif III I

10 11 12 13 14

Порог 41

Рис. 15.7. Синдромно-пороговый декодер для ОСР-кода, п = 15.

ных сумматоров и пороговый элемент с семью входами, выход кото- рого равен 1 тогда и только тогда, когда не менее пяти из его вхо-"! дов равны 1. Декодер, изображенный на рис. 15.7, называете* синдромным пороговым декодером, так как входы порогового элемента представляют собой символы синдрома + -\- R, Rq + R, + + i?8, . . ., Rq +-ffii + ?i2, значения которых равны соответственно! Ео + + Е, Ео + Е + Eg, . . ., Ео + Е + Е. Выход поро гового элемента равен принимаемой величине символа Eg.

Алгоритмы декодирования с исправлением t ошибок (рис. 15.4-15.7) используют существование 2t проверочных соотношений, орте тональных на декодируемой позиции. Для большинства кодов исправляющих t ошибок, не существует 2t проверочных уравнений,! ортогональных на любой заданной позиции. Однако, как показывает следующий пример, иногда мажоритарное решение позволяет опреден лить вектор ошибок, если использовать в декодере многостуненчат5 процедуру.

15.46. Двухступенчатое пороговое декодиро в а н и е РМ- (31,16)-к ода. Рассмотрим 1-укороченный код вто рого порядка с блоковой длиной 31, исправляющий 3 ошибки. Mi покажем, что этот код можно декодировать с помощью синдромног порогового декодера рис. 15.8, где связи внутри «цепей суммирова ния» могут быть определены из рис. 15.9 способом, который буде объяснен ниже.

Задачей всех цепей на рис. 15.8 является получение величины символа £"0 вектора шума. Как только это будет сделано, символ п нулевой позиции может быть исправлен, и, используя циклический сдвиг, на той же схеме можно будет получить величины

Ei, Е2, . . ., £n-i-

Величина Eg получается как выход оконечного порогового элемента с шестью входами. Каждый вход этого оконечного порогового элемента равен двоичной сумме четырех символов вектора ошибки, соответствующих одному из множеств, указанных в крайнем

Из канала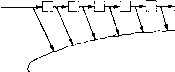

1Q3T

Схема сложения

пороговые элементы

) (тЛ) (гГзГ) (Н® £)

Оконечный, пороговый аяемент

Рис. 15.8. Двухступенчатый декодер для РМ-(31,16)-кода1

leBOM столбце верхней таблицы на рис. 15.9. На первый вход подается величина £0 + 4 + 12 + 15; на второй £0+8 + 24 +

г- £30, . . ., на шестой £о + £9 + £п + £18-

Каждая из четверок на рис. 15.9 определяет аффинное подпро-(транство в GF (2). Любые две четверки из одной и той же строки лгогут быть переведены друг в друга. Следовательно, объединение любых двух четверок из одной и той же строки на рис. 15. 9 определяет трехмерное аффинное подпространство в GF {2). Например, объеди-пение первых двух четверок на рис. 15.9 дает {О, 4, 12, 15, 1, 17, 13}, что соответствует трехмерному аффинному подпространству

{а\ а\ а}\ а}\ а, а", а\ а"}.

Используя приложение А, читатель может проверить, что это действительно аффинное подпространство. Согласно теоремам 15.323 н 15.329, код удовлетворяет проверочному соотношению, которое определяется fлюбым трехмерным аффинным подпространством, не содержащим а. Иными словами, декодер может вычислять символы

Рис. 15.9. Аффинные подпространства пространства GF (2).

синдрома

Si = i?0 + 4 + Е-, + J15 + 1 + 17 + 8 + J13

1,ак суммы

si = i?o + -ff* + + Rib + Ri + Ri7 + Rs + Ri3-

\палогично может быть вычислена двоичная сумма ошибочных символов в позициях {О, 4, 12, 15, 2, 22, 27, 9}, {О, 4, 12, 15, 3, 25, И, 28}, . . ., {О, 4, 12, 15, 19, 26, 29, 21}. Так как эти шесть проверочных соотношений ортогональны на {О, 4, 12, 15}, то при условии, что и канале произошло не более трех ошибок, выход первого предварительного порогового элемента равен Eg -\- Е + £"15-

Каждый из шести предварительных пороговых элементов определяет соответственно величину двоичной суммы ошибочных симво-.гов, указанных в крайнем левом столбце верхней таблицы рис. 15.9. 1"]сли в канале произошло не более трех ошибок, то каждая из этих величин правильна и выход оконечного порогового элемента дает правильное значение символа Eg. Если в канале произошло четыре или более ошибок, то декодер рис. 15.8 может произвести как пра-зшльное, так и ошибочное декодирование (см. задачу 15.5).

Декодер рис. 15.8 осуществляет двуступенчатое пороговое декоди-])ование, так как рассматриваемый код ортогонализируем в два шага 1! соответствии со следующим определением.

15.47. Определение. Линейный код, исправляющий t ошибок, называется ортогонализируемым в 1 шаг, если для него существует 2t проверочных уравнений, ортогональных на каждой позиции /, i = О, 1, 2, . . ., п - I.

Код называется ортогонализируемым в L шагов, если существуют шожества позиций Р(), Р(), . . ., такие, что:

1) для всех i код имеет 2t проверок, ортогональных на

2) подкод исходного кода, удовлетворяющий этим проверкам ( 2 =0 для всех i}, ортогонализируем ъ L - 1 шаг.

Для РМ-кода порядка г и длины 2" - 1, исправляющего 2"""i-1 огаибок, в качестве множеств Р() могут быть выбраны г-мерные аффинные подпространства пространства GF (2""). Подкод, удовлетворяющий проверкам С- = О для всех i, является РМ-кодом

3-£p(i)

порядка г - 1. Отсюда непосредственно (индукция по г) вытекает следующее утверждение:

15.48. Теорема. РЖ-код порядка г с длиной 2, исправляю-ищй (2"""1 - 1) ошибок, и 1-укороченный РЖ-код порядка г с длиной 2 - 1, исправляющий (2"~" - 1) ошибок, ортогонализируемы в г 1 шагов; 2-укороченный РЖ-код порядка г с длиной 2*"- 1, исправляющий (2"~~ - 1) ошибок, ортогонализируем в г шагов.

Как видно из примера 15.46, некоторые РМ-коды порядка" ортогонализируемы меньше чем в г -f- 1 шагов. Однако ни один не 2-укороченных РМ-кодов при г > 1 не допускает ортогонализацик> в один шаг.

Для некоторых кодов, исправляюш;их несколько ошибок и допу-1 екающих ортогонализацию в несколько шагов, пороговое декодиро-j ванне хуже алгебраических процедур декодирования. Например,! коды Хэмминга являются 1-укороченными РМ-кодами, и поэтому к ним применимо пороговое декодирование. Однако такие декодеры! оказываются сложнее, чем декодер, схема которого нредставлена на рис. 5.3.

С другой стороны, для многих легко ортогонализируемых кодов! с исправлением t ошибок пороговые декодеры значительно проще] реализуемы, чем алгебраические. К сожалению, для большинства; кодов легкая ортогонализация неосуществима, а у тех кодов, кото- рые легко ортогонализируемы, минимальное расстояние значительно! хуже минимального расстояния сравнимых БЧХ-кодов. Во многих! случаях, однако, эти недостатки порогового декодирования окупа- ются преимуществами легкой реализации. В случаях, когда помимо! всех ошибок веса t необходимо исправлять многие ошибки более] высокого веса, преимущества порогового декодирования еще больше.-Как отмечалось в разд. 10.5, алгебраические алгоритмы декодирова- ния требуют в этих случаях введения дополнительных остроумных! правил. Пороговые алгоритмы позволяют исправлять многие ошиб- ки веса > t автоматически.

15.5. Ортогонализируемые коды, основанные на конечных геометриях!

Относительная простота некоторых пороговых декодеров послу-] жила стимулом к поиску кодов, ортогонализируемых в малое число! шагов. Этот поиск привел к открытию нескольких важных классов! ортогонализируемых кодов, включающих квазициклические коды! Таунсенда - Велдона [1967], евклидово-геометрические коды и про- ективно-геометрические коды.

Впервые некоторые проективно-геометрические коды исследовал! в конце 1950 г. Прейндж. Им были получены многие результаты! о распределении весов кодовых слов и лидеров смежных классов! для некоторых двоичных кодов, основанные на использовании про-Г ективных геометрий, а также подстановок, относительно которых? эти коды инвариантны. К сожалению, эти работы Прейнджа не были опубликованы. В 1966 г. Велдон ввел в рассмотрение разностные коды, являющиеся подклассом проективно-геометрических кодов. Более общие классы кодов, основанные на конечных геометриях, были предложены Рудольфом [1964, 1967]. Дальнейшие результаты] в этой области были получены Чоу [1967], Гёталсом и Делзартом [1968], Грэхемом и Мак-Вильямс [1966], Мак-Вильямс и Манном! [1968], Смитом [1967, 1969] и Велдоном [1968 а, Ь].

К сожалению, в работах этих авторов одни и те же обозначения имеют разный смысл. Приводимые ниже определения охватывают только работы автора.

15.51. Определения. Евклид ово-геометрическим кодом (ЕТ-кодом) над GF (р) порядка {г, s) длины п = р™ называется код, дуальный к подкоду над подполем GF (р) ОРМ-кода над GF (q) порядка [{q - 1) (m - г - 1)] {q = р").

15.52. Теорема. Минимальное расстояние ЕТ-кода порядка {г, s) не меньше d = (g"" - l)/{q - 1). Этот код ортогонализируем 3(1 (г + 1) шаг.

Доказательство. Согласно теоремам 11.61 и 15.329, .характеристическая функция каждого (г 4- 1)-мерного подпространства из GF (q) над GF (q) является кодовым словом ОРМ-кода порядка [{q - i) (т - г - 1)]. Так как все координаты таких кодовых слов равны О или 1, то эти слова также принадлежат под-1;оду ОРМ-кода над подполем GF (р). Следовательно, ЕГ-код г поряд-i;a (г, s) удовлетворяет проверочному соотношению на каждом (r-f-

1)-мерном аффинном подпространстве.

Каждое заданное г-мерное аффинное подпространство в GF {q") ]шд GF {q) имеет q™ линейных сдвигов. Данное г-мерное аффинное подпространство и любой из его q~ - 1 непересекающихся с ним сдвигов лежат в некотором (г -- 1)-мерном аффинном подпространстве, состоящем из г-мерного подпространства и g - 1 его линейных сдвигов. Следовательно, существует d различных (г -f 1)-мерных аффинных подпространств, содержащих любое заданное г-мерное аффинное подпространство. Характеристические функции этих аффинных подпространств образуют множество d проверочных уравнений, ортогональных на данном г-мерном подпространстве.

Таким образом, если в канале произошло не более d/2 ошибок, то декодер для ЕГ-кода порядка (г, s) может вычислить проверки на нсех г-мерных аффинных подпространствах с помощью одного ,\ровня пороговых элементов. Индукция по г завершает доказательство теоремы, щ

15.53. Определение. Пусть а - примитивный элемент Г/0.1Я GF (q), q = р", а V - циклический код над GF (q), корни порождающего многочлена которого имеют вид а<") % Wq ([?-l]i) > > г (g-1), где Wq (х) - сумма цифр в q-ичном разложении числа х. Тогда р-ичным проективно-геометрическим кодом (ПГ-ко5ол1) порядка (г, s) с блоковой длиной п = (д™ -1)/(д-1) называется код, дуальный к подкоду кода V над подполем GF (р).

15.54. Теорема. Минимальное расстояние р-ичного ИТ-кода >1орядка (г, s) равно по меньшей мере d = (g" - l)/(g - 1), где Ч = Этот код ортогонализируем в г шагов.